問1~2、問4に関しては以下のページに解説をまとめているので参考にして下さい。
図のように円周上に3点 A、B、C があり、∠OAC=15°、∠OBC=55°、円の半径が6cmであるとき、以下の問いに答え なさい。
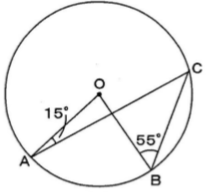
[問題1] ∠ACBの角度を求めなさい。
[解答群]
ア 50° イ 30° ウ 40° エ 45° オ 35°
[問題2] ∠ACBに対する円弧ABの長さを求めなさい。
[解答群]
ア 10 cm イ 7 cm ウ 9/4 cm エ (8/3)π cm オ 7/2 cm
[問題3] 扇形AOBの面積を求めなさい。
[解答群]
ア 8π cm² イ 10π cm² ウ (21/2)π cm² エ 14π cm² オ (27/5)π cm²
解答と解説
試験問題1の解答:ウ
求めたい∠ACBをX°と仮定します。∠AOBは∠ACBの2倍の角度なので次の式が成り立ちます。
∠ACB=X
∠AOB=2X
OBとACの交点をQとした場合、∠OQA=∠BQCなので、この角をY°とした場合次の式が成り立ちます。
三角形OAQの内角
15+2X+Y=180
2X+Y=165 ・・・(1)
三角形BCQの内角
55+X+Y=180
X+Y=125 ・・・(2)
2X+Y=165 ・・・(1)
X+Y=125 ・・・(2)
———————-
X=40°
試験問題2の解答:エ
∠ACBに対する円弧ABは、∠AOBに対する円弧ABと同じ。問題1より∠ACB=40°とわかっているので∠AOB=80°となり、AOBは円の1/4.5の扇型だと分かります。
円は半径6㎝の円なのでその円周は次の通り。
(6+6)xπ=12π
円弧ABはこの円周の1/4.5なので求めたい円弧ABは次の通り。
12π/4.5=120π/45=8π/3 ㎝
試験問題3の解答:ア
半径6㎝の円の面積は次の通り。
6x6xπ=36π
更に問題1より扇型AOBは∠AOB=80°で円を1/4.5にした大きさだと分かっています。よって、扇型AOBの面積は次の通り。
36πx(1/4.5)=8π ㎝²
※解説を記載するまでもないと判断した問題に関しては、解説を記載せず解答のみを記載しています。もし、この問題の解説が欲しいというのがあれば、コメント欄に記載してください。また、記載している解説の内容も不明であれば遠慮なくコメントください。

