次の問に答えなさい。

[問題1]座標平面上の２点，Ａ(－３,－４)，Ｂ(５,２)の中点の座標を求めなさい。

[問題2]ある晴れた日に、木の影の長さをはかると130cmあり、身長152cmのＡ君の影の長さをはかると38cmありました。このとき、木の高さは何ｍですか？

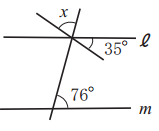東京 職業訓練問題[問題3]右図において，ℓ∥m のとき，∠x の大きさは何度ですか？

[問題4]ある野球チームの打者が16打席目にヒットを打ったところ、15打席終了時点より打率が３分７厘５毛（0.0375）上がりました。このとき、この打者の16打席終了時点の打率は何割何分何厘何毛ですか。ただし，打率の計算は（ヒット数）÷（打席数）とします。

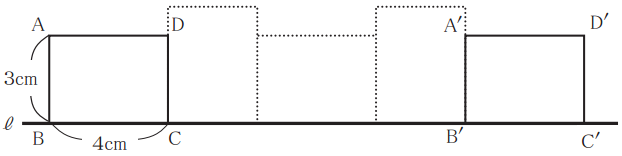
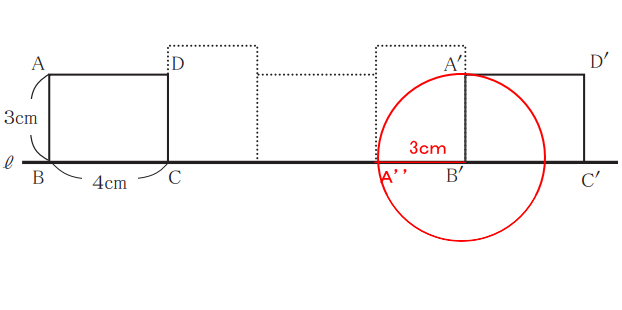
[問題5]下図のように、ＡＢ＝３cm、ＢＣ＝４cmの長方形ＡＢＣＤを直線ℓ 上を滑ることなく転がして１回転させ、長方形Ａ′Ｂ′Ｃ′Ｄ′の位置まで移動させます。このとき、頂点Ａが移動した距離の合計は何cmですか？
東京職業訓練試験

解答と解説

試験問題１の解答：
2点の座標の中点、いわゆる2点の中間にある座標を求めるのですが、これは難しく考える必要は無い。2点のＸ座標どうしを足して2で割った値が中点のＸ座標となる。同様に2点のＹ座標どうしを足して2で割った値が中点のＹ座標となる。

　２点，Ａ(－３,－４)，Ｂ(５,２)より、

　中点のＸ座標は、(-3+5)÷2 ＝ 1
　中点のＹ座標は、(-4+2)÷2 ＝ -1

よって、求める中点の座標は、(1, -1)となる。

解答：(1, -1)

試験問題２の解答：
身長152cmのＡ君の影の長さが38cmなので、影の長さ38cmを身長の152cmで割ると、身長1cmあたりの影の長さが求まります。

　38÷152＝0.25cm

よって、高さ1cmあたり0.25cmの影ができることになる。130cmの影ができるには、

　130÷0.25＝520cm

520cm(130cmは、0.25cmの520倍ということ)の高さが必要になることが分かる。求められているのは、何ｍか？なので、求める解答は、5.2mとなる。

解答：5.2m

試験問題３の解答：
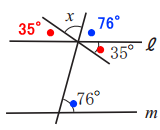角度向かい合う角は等しいので、●の角度は等しくなります。更に、直線ℓとmが平行する場合、●の角度も等しくなる。

また、直線ℓの上にある●35°と、●76°、Ｘの角度の合計は180度になる。よって、次の式が成り立つ。

　35+76+X＝180
　X＝180-35-76
　X＝69度

よって、求める解答は、69度

解答：69度

試験問題４の解答：
求める16打席目の終了時点の打率をＮとします。
16打席目の終了時点で打ったヒット数をＨとします。

このＮとＨを利用し、15打席目終了時点と、16打席目終了時点を式になおします。

15打席目終了時点
設問の内容より、下記のことがわかります。
　ヒット数：Ｈ-1
　打席数：15
　打率：Ｎ-0.0375

打率＝（ヒット数）÷（打席数）より、

　Ｎ-0.0375 ＝ (Ｈ-1) ÷ 15 ・・・（１）

16打席目終了時点
　ヒット数：Ｈ
　打席数：16
　打率：Ｎ

打率＝（ヒット数）÷（打席数）より、

　Ｎ ＝ Ｈ ÷ 16
　Ｈ ＝ 16Ｎ ・・・（２）

この式（２）を式（１）に代入し、計算すると求めたい打率Ｎを出すことができる。

　Ｎ-0.0375 ＝ (16Ｎ-1) ÷ 15
　(Ｎ-0.0375) x 15 ＝ 16Ｎ-1
　15Ｎ-0.5625 ＝ 16Ｎ-1
　Ｎ ＝ 1-0.5625 ＝ 0.4375

よって、求める16打席目の終了時点の打率は、4割3分7厘5毛となる。

解答：4割3分7厘5毛

試験問題５の解答：
下図のように最初の1回転目に着目してみてみます。

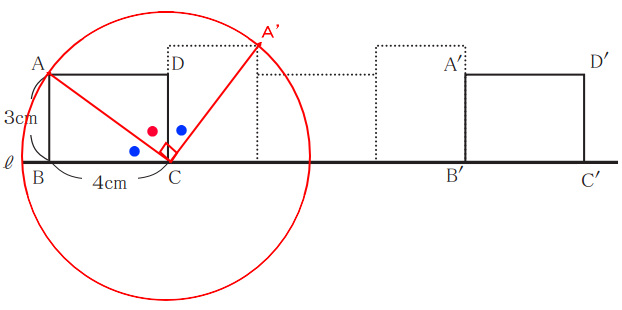
職業訓練 角度問題

頂点Ａは、最初の1回転目で頂点Ｃを中心とした円の弧に沿って回転したことがわかります。また、●の∠ＡＣＢと∠Ａ´ＣＤは、同じ場所なので同じ角度だと分かります。更に●と●の角度を足すと90度になるので、頂点Ａが頂点Ａ´まで移動した角度は90度となる。

よって、頂点Ｃを中心とした円の円周の長さを4分の1したものが、最初の1回転で頂点Ａが移動した距離となる。円周を求める公式は、下記の通り。

　円周 ＝ 直径 ｘ Π

しかし、現時点で円の直径が分かっていない。ＡＣは円の半径なのでＡＣの長さが分かれば、円の直径も分かる。ここで利用するのが、三平方の定理の公式です。

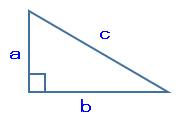
三平方の定理とは、下図の様な直角三角形の各辺の長さは、次の式で表すことができます。

　ａ² ＋ ｂ² ＝ ｃ²

三平方の定理

この三平方の定理より、次の式が成り立つ。

　半径ＡＣ² ＝ 3² + 4²

この式を解くと、半径ＡＣが出てきます。

　半径ＡＣ² ＝ 3² + 4² ＝ 9 + 16 ＝ 25
　半径ＡＣ ＝ 5cm

よって、円の直径は、5cmｘ2cm＝10cmだと分かる。円の円周の長さは

　円の円周 ＝ 10Π

であり、この4分の1が移動した距離なので、

　頂点Ａが移動した距離 ＝ 10Π ÷ 4 ＝ 2.5Π ・・・（１）

となる。これが1回転目で移動した距離になる。次に2回転目に着目して見てみます。2回転目は、下図の様に頂点Ａ´から頂点Ａ´´まで、半径4cmの円の円周を移動したことが分かります。よって、移動した距離は、

　円の円周 ＝ 4 x 2 x Π ＝ 8Π
　頂点Ａ´の移動距離 ＝ 8Π ÷ 4 ＝ 2Π ・・・（２）

次に3回転目だが、3回転目は頂点Ａは円の中心になるため、移動距離は０。最後の4回転目は、下図の様に半径3cmの円周上を動くことが分かります。

職業訓練試験問題
　円の円周 ＝ 3 x 2 x Π ＝ 6Π
　頂点Ａ´´の移動距離 ＝ 6Π ÷ 4 ＝ 1.5Π ・・・（３）
　
よって、求めたい頂点Ａの総移動距離は、（１）（２）（３）の合計となる。

　2.5Π + 2Π + 1.5Π ＝ 6Π

解答：6Π