平成27年度に埼玉県で実施された職業訓練の選考試験で出題された試験問題と、その解答と解説です。 本ページでは数学問題の設問1(正式なテスト用紙上では設問4)のみ記載しています。数学問題の設問2~3に関しては、以下のページを参照してください。
埼玉 職業訓練 試験問題[長期] 数学-問2(平成27年入校生)
埼玉 職業訓練 試験問題[長期] 数学-問3(平成27年入校生)
試験問題 設問1
次の(1)~(10)の計算をしなさい。
[問題1]
-29-38=
[問題2]
56-3×9=
[問題3]
24÷3+5×3-9=
[問題4]
45×0.8=
[問題5]
(2/5)-(1/3)=
[問題6]
(2/3)÷(4/5)=
[問題7]
[問題8]
4a²b×3bc²÷6abc²=
[問題9]
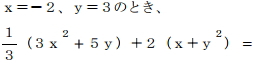
[問題10]
2次不等式 X²-2X-8<0 の解を求めなさい。
解答と解説
試験問題1の解答:-67
試験問題2の解答:29
試験問題3の解答:14
試験問題4の解答:36
試験問題5の解答:
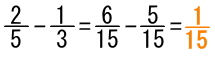
試験問題6の解答:
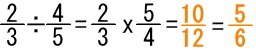
試験問題7の解答:
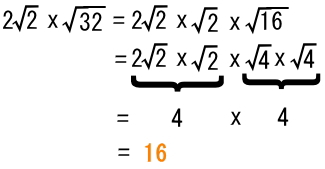
試験問題8の解答:
4a²b×3bc²÷6abc²
=12a²b²c²÷6abc²
=12a²b²c²/6abc²
=2ab
試験問題9の解答:
(3x²+5y)/3 + 2(x+y²)=
x=-2、y=3を代入する
(3x²+5y)/3 + 2(x+y²)
=(12+15)/3 + 2(-2+9)
=27/3 + 14
=9 + 14
=23
試験問題10の解答:
この問題は、因数分解ができることが必須となる。
X²-2X-8<0 を因数分解すると下記のようになる。
(X-4)(X+2) < 0
2次方程式であれば、X=4 、-2 となるのだが、今回の問題は2次不等式です。Xの値ではなく、Xの取り得る範囲を求めないといけない。2次方程式のグラフを描いてみると分かり易いのだが、いちいちグラフを描いていると時間がたりなくなる。よって、下記の法則は覚えておいて欲しい。
(x±α)(x±β)<0のときはα<x<β (α<β)
(x±α)(x±β)>0のときはx<α、x<β (α<β)
「(X-4)(X+2) < 0」の「<」は右開きなので上記2つの法則の上の方に該当する。
よって、求める解答は、 -2 < X < 4 となる。
※注意
「4 < X < -2」のように逆にしないように。Xの値が4よりも大きく-2より小さいといった数値は存在しない。法則は「α<β」なので今回の場合であればαが-2、βが4となる。

