問1~2、問4に関しては以下のページに解説をまとめているので参考にして下さい。
図のように、∠A=30°、∠C=90°の直角三角形ABCとその内接円がある。点D、E、Fは接点で、点Dから線分EFに垂線DHを引く。DC=4のとき、以下の問いに答えなさい。
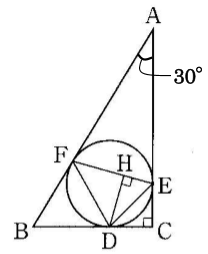
[問題1] ∠DEFの角度を求めなさい。
[解答群]
ア 30° イ 45° ウ 70° エ 55° オ 60°
[問題2] 線分DHの長さを求めなさい。
[解答群]
ア 6 イ 2√6 ウ 10 エ 4√6 オ 2√2
[問題3] △DEFの面積を求めなさい。
[解答群]
ア 12+4√3 イ 96 ウ 32+24√2 エ 18√2+12√3 オ 132
解答と解説
試験問題1の解答:オ
三角形に円が内接する場合、三角形の各頂点から円に接する2点までの距離までは等しくなります。このことより次のことが言えます。
△AFEは二等辺三角形
△BDFは二等辺三角形
△CEDは二等辺三角形
よって、∠AEFと∠CEDは次の角度になります。
∠AEF=(180-30)÷2=75°
∠CED=(180-90)÷2=45°・・(1)
よって、∠DEFは次の通り。
∠DEF=180-75-45=60°
試験問題2の解答:イ
この問題を解く上で覚えておきたいのが直角三角形の各辺の比についてです。
直角二等辺三角形の各角度が、90°、45°、45°となる場合、各辺の比率は、「1:1:√2(斜辺)」となります。更に直角二等辺三角形の各角度が90°、60°、30°となる場合、各辺の比率は「1:2(斜辺):√3」となります。
△CEDは問題1の(1)より、内角が90°、45°、45°となる直角三角形と分かり、各辺の比率は「1:1:√2」となります。更にDC=4とわかっているので、辺DEの長さは次の通り。
4x√2=4√2・・(2)
次に問題1より、∠DEFは60°と分かっています。∠EHDは90°なので、△DEHは内角が90°、60°、30°の直角二等辺三角形で各辺の比率が「1:2:√3」になります。よって、線分DHの長さは次の通り。
EH:DE:DH=1:2:√3
DE:DH=2:√3
DH=(√3/2)xDE
=(√3/2)x4√2
=2√6
試験問題3の解答:ア
問題2で触れた△DEHの各辺の比率についてもう一度見てみます。
EH:DE:DH=1:2:√3
DEの長さは問題2の(2)より、4√2だと分かっています。EHとDEの長さ比は1:2なので、EHの長さはDEの半分の長さだとわかります。よって、EHの長さは次の通り。
EH=4√2/2=2√2
また、∠CDE=45°、∠EDH=30°、∠BDF=60°と分かっているので、∠HDFは次の通り。
∠HDF=180-45-30-60=45°
更に∠DHF=90°なので、△DHFは直角二等辺三角形だと分かります。よって、HFの長さはDHと同じ2√6になります。
よって、EFの長さは次の通り。
EFの長さ=EH+HF
=2√2+2√6
よって、△DEFの面積は次の通り。
△DEF面積=EFxDH÷2
=(2√2+2√6)x2√6÷2
=2√12+12
=12+4√3
※解説を記載するまでもないと判断した問題に関しては、解説を記載せず解答のみを記載しています。もし、この問題の解説が欲しいというのがあれば、コメント欄に記載してください。また、記載している解説の内容も不明であれば遠慮なくコメントください。

