大阪 職業訓練 試験問題 数学-問3(平成28年8月25日実施) 短期課程

ｙ＝ｘ²/4上の2点A、Bのx座標をそれぞれ－2、4とする。2点A、Bを通る直線ℓのx軸、ｙ軸との交点をそれぞれC、Dとする。以下の問いにア～オから選んで答えなさい。

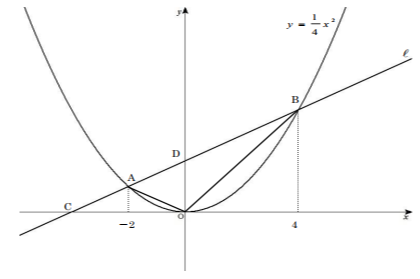
[問題1]　直線ℓの式を求めなさい。

[問題2]　三角形 OAB の面積を求めなさい。

解答と解説

試験問題１の解答：エ
点Aの座標を求める
点Aのｘ座標は-2と分かっているので、放物線の式にこの値を代入するとｙ座標が求まります。

ｙ＝ｘ²/4
　＝4/4
　＝1

点Aの座標(-2,1)

点Bの座標を求める
点Bのｘ座標は4と分かっているので、放物線の式にこの値を代入するとｙ座標が求まります。

ｙ＝ｘ²/4
　＝16/4
　＝4

点Bの座標(4,4)

直線ℓの式を求める
直線ℓの傾きをａ、ｙ軸との交点のｙ座標をｂとした場合、直線は次の式で表すことができます。

ｙ＝ａｘ+ｂ

この直線は点A、点Bを通るので上記の式にそれぞれの値を代入してａとｂの値を求めていきます。

点Aの座標(-2,1)を代入
1＝-2ａ+ｂ ・・・(１)

点Bの座標(4,4)を代入
4＝4ａ+ｂ ・・・(２)

(２)-(１)をするとａの値が求まります。

4＝4ａ+ｂ ・・・(２)
1＝-2ａ+ｂ ・・・(１)
——————-
3＝6ａ
ａ＝1/2

ａの値がわかったので、これを(１)もしくは(２)に代入し、ｂの値も求めます。

1＝-2ａ+ｂ ・・・(１)
1＝-2×1/2+ｂ
1＝-1+ｂ
ｂ＝2

よって、直線ℓの式は次の通り。

ｙ＝ｘ/2+2

試験問題２の解答：イ
三角形OABの面積は三角形OADと三角形OBDの2つに分けて考える。

三角形OADの面積を求める
点Dの座標は問題１の直線ℓの式より、(0,2)だとわかります。よって、底辺をODとした場合、その長さは2となります。高さは点Aのｘ座標になるので2。ｘ座標は-2だが、距離(高さ)として扱うので絶対値の2として考える。よって、三角形OADの面積は次の通り。

面積＝2ｘ2÷2＝2

三角形OBDの面積を求める
底辺は三角形OADと同じODとして考えます。よって、その長さは2。高さは点Bのｘ座標になるので4。よって、三角形OBDの面積は次の通り。

面積＝2ｘ4÷2＝4

三角形OABの面積を求める
△OAB面積＝△OAD面積+△OBD面積
△OAB面積＝2+4＝6

※解説を記載するまでもないと判断した問題に関しては、解説を記載せず解答のみを記載しています。もし、この問題の解説が欲しいというのがあれば、コメント欄に記載してください。また、記載している解説の内容も不明であれば遠慮なくコメントください。