次の計算をしなさい。ただし,(5),(6)は小数で,(7)は分数で求めなさい。
[問題1] 38+286=
[問題2] 311-79=
[問題3] 63x27=
[問題4] 874÷19=
[問題5] 39.3+25.8=
[問題6] 4.7×3.5=
[問題7]
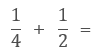
[問題8]
![]()
[問題9] 6a²bc x 2ab²c² ÷ 4a³bc=
[問題10] x²-8x-33=0 のとき、x(x≧0)の値を求めなさい。
解答と解説
試験問題1の解答:324
試験問題2の解答:232
試験問題3の解答:1701
試験問題4の解答:46
試験問題5の解答:65.1
試験問題6の解答:16.45
試験問題7の解答:
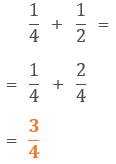
試験問題8の解答:
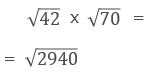
ルートから出せるものは出すようにしましょう。
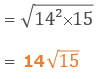
試験問題9の解答:
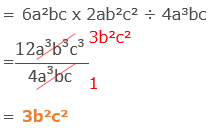
試験問題10の解答:X=11
この問題は、因数分解ができることが必須となる。
足して-8、掛けて-33になる2つの数値を探す。掛けた場合、-33と値がマイナスなので2つの数値の内、いずれか一方がマイナスであることは直ぐにわかるが、まずはマイナス、プラス意識せずに掛けて33になる2つの数値を探してみる。
そうすると、1と33、3と11の2組だと分かる。次に足して-8となる組み合わせを考える。1と33の組み合わせの方は、どちらか一方の数値にマイナスを付けて足し算をしても-8になることはないので違う。3と11の組み合わせの方は、11をマイナスとした場合、2つの数値を足すと3-11=-8になるのでこの組み合わせが正しい。
よって、因数分解すると次のようになる。
(X+3)(X-11)=0
このことより、X=-3と11 だと分かる。しかし、設問に X≧0 とあるので、求める解答は、X=11となる。
※解説の内容が不明、不十分というのがあればコメントをください。

