この問題は平成28年4月入校の東京都立職業能力開発センター入校選考試験問題の問2の(5)の解答と解説です。
問1および、問2の(1)~(4)に関しては以下のページに解説をまとめているので参考にして下さい。
実際の試験の問題用紙は以下のページで確認することができます。
試験問題 問2(5)
図のような、円すいの展開図があります。円すいの頂点となる点Aから底面の中心Oまでの距離が11cmのとき、この円すいの体積は、何cm³ですか。
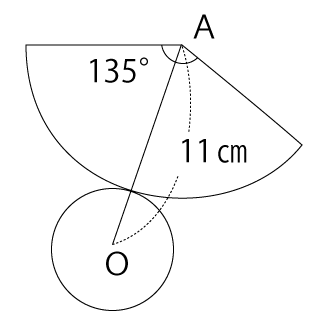
解答と解説
問2(5)の解答:3√55π
この問題を解くには以下の4つの点について知っている必要があります。
解くのに必要な知識
- 円すいの体積を求める公式
- 三平方の定理
- 円周を求める公式
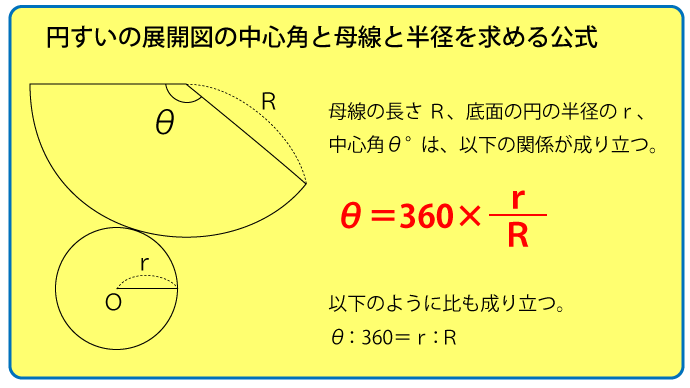
- 円すいの展開図の中心角と母線と半径を求める公式(任意)
以下の4つ目の『円すいの展開図の中心角と母線と半径を求める公式』を知っていれば短時間で解くことが可能ですが、覚えている人も少ないと思うので今回はこの公式を使わずに解説します。
解答までの求め方の流れは次の通りです。
求め方の流れ
- 扇形と円の半径を求める
- 円すいの高さを求める
- 円すいの体積を求める
扇形と円の半径を求める
下図のように扇形の半径をRと仮定します。
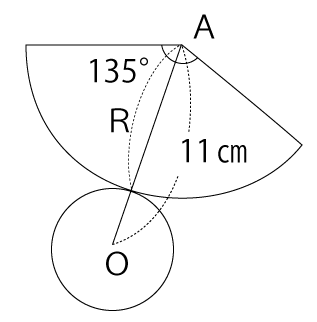
このとき、扇形の弧の長さは次の通りになります。
扇形の弧の長さ=直径×π×(135/360)
=2Rπ×3/8
=3Rπ/4・・・①
扇形の半径がRなので、底面の円の半径は11-Rとなります。よって、この円の円周の長さは次の通りになります。
円の円周の長さ=直径×π
=(11-R)×2×π
=22π-2Rπ・・・②
扇形の弧の長さと円の円周の長さは等しいので次の式が成り立ちます。
①=②
3Rπ/4=22π-2Rπ
3R/4=22-2R
3R=88-8R
11R=88
R=8
よって、扇形の半径は8cm、円の半径は3cmとなります。
円すいの高さを求める
円すいの高さは三平方の定理を利用して求めます。
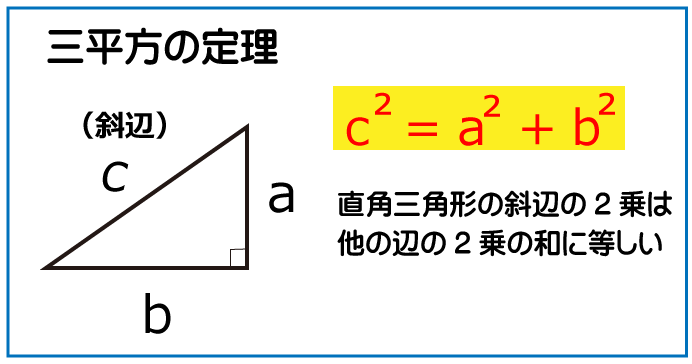
円すいを真横から見ると下図のようになります。
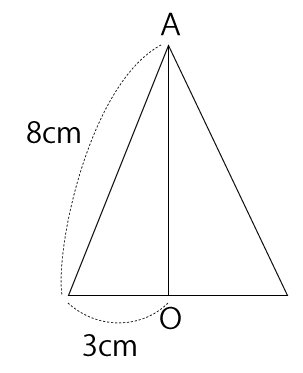
三平方の定理より、以下の式が成り立ちます。
8²=3²+AO²
AO²=64-9
=55
AO=√55
円すいの体積を求める
円すいの体積を求める公式は次の通り。

円すいの底面の円の半径は3cm、円すいの高さは√55と分かったので、公式より体積は次の通りになります。
円すいの体積=底面積×高さ÷3
=(3×3×π)×√55÷3
=9π×√55÷3
=3√55π
※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。

