【福岡県】職業訓練校 入校選考試験問題サンプル問題の解答と解説

この問題は福岡県の職業訓練校・福岡県立高等技術専門校が公開している普通課程の入校選考試験サンプル問題とその解説です。問題はサンプルですが、実際の試験はほぼ同レベルで似た問題が出題されるので、必ずすべて解けるようになるまで何度も繰り返し実施するようにしてください。

⇒福岡県立高等技術専門校（普通課程）入校選考試験問題【サンプル】

問１の問題

数と式の計算問題（５者択一式）

【１】5/3÷(1/2＋2/3)を計算しなさい。

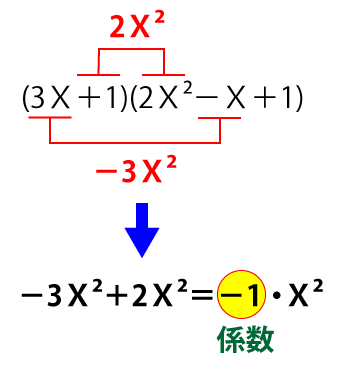
【２】(3Ｘ＋1)(2Ｘ²－Ｘ＋1)を展開したときのＸ²の係数を求めなさい。

解答と解説

問１【１】の解答：10/7

計算の優先順位は割り算よりも括弧内の足し算の方が高い。

5/3÷(1/2＋2/3)
＝5/3÷(3/6＋4/6)
＝5/3÷7/6
＝5/3×6/7
＝10/7

問１【２】の解答：－1

(3Ｘ＋1)(2Ｘ²－Ｘ＋1)
＝6Ｘ³－3Ｘ²＋3Ｘ＋2Ｘ²－Ｘ＋1
＝6Ｘ³－Ｘ²＋2Ｘ＋1

よって、Ｘ²の係数は『－1』

試験時間は必ず不足してくるので、できれば上記のように完全に展開してしまうのではなく、下記のようにＸ²になる部分だけを抜き出して計算できるようにしておきたいところです。

問２の問題

方程式・不等式の問題（５者択一式）

【１】2次方程式Ｘ²－7Ｘ＋3＝0を解きなさい。

【２】連立方程式2Ｘ＋1＜3、3Ｘ－2≧－8を解きなさい。

解答と解説

問２【１】の解答：(7±√37)/2

Ｘ²－7Ｘ＋3＝0

上記の式を以下のように変換できるかが重要です。これは数をこなしてなれるしかありません。

(Ｘ－7/2)²－49/4＋3＝0
(Ｘ－7/2)²－49/4＋12/4＝0
(Ｘ－7/2)²－37/4＝0
(Ｘ－7/2)²＝37/4
Ｘ－7/2＝±√37/2
Ｘ＝7/2±√37/2
Ｘ＝(7±√37)/2

また、この問題は解の公式を使っても解くことが可能です。できれば、この解の公式を覚えておいた方が問題を解く時間も短縮できます。

問２【２】の解答：－2≦Ｘ＜1

2Ｘ＋1＜3
3Ｘ－2≧－8

上記2つの連立不等式を計算し簡素します。

2Ｘ＋1＜3
2Ｘ＜3－1
2Ｘ＜2
Ｘ＜1・・・①

3Ｘ－2≧－8
3Ｘ≧－8＋2
3Ｘ≧－6
Ｘ≧－2・・・②

不等式①②を図式化すると下図のようになります。

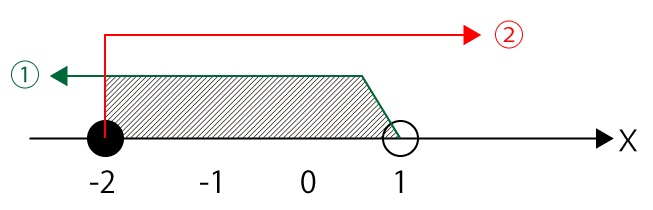
よって、Ｘの取り得る範囲は、－2≦Ｘ＜1

問３の問題

2次関数・三角比・データの分析の問題（５者択一式）

【１】 関数f(Ｘ)＝Ｘ²＋3Ｘ－7において、f(−2)の値を求めなさい。

【２】7個のデータ，71, 73, 69, 73, 70, 74, 71 の中央値を求めなさい。

解答と解説

問３【１】の解答：－9

f(Ｘ)＝Ｘ²＋3Ｘ－7

Ｘ＝－2なので上記の式のＸに－2を代入します。

f(－2)＝(－2)²＋3(－2)－7
　　　＝4－6－7
　　　＝－9

問３【２】の解答：71

この問題で間違いやすいのが平均値を求めてしまうことです。中央値と平均値は異なります。

平均はデータを合計してその合計をデータ個数で割った値ですが、中央値はデータの順番を並び替えて丁度真ん中にくる値です。

よって、今回の問題であれば7個のデータがあるのでデータを昇順もしくは降順に並び替えて4番目にくるデータが中央値になります。

71, 73, 69, 73, 70, 74, 71
↓
69, 70, 71, 71, 73, 73, 74

よって、中央値は71

問４の問題

図形と計量及びその他の問題（数字選択式）

【１】1/(√5＋√3)は分母を有利化すると (√①－√②)/③ になる。①②③には一桁の整数が入る。

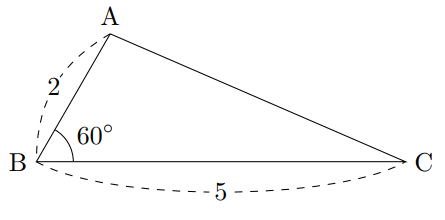
【２】図の三角形ABCにおいて、AB＝2、BC＝5、∠ABC＝60◦である。このとき、辺ACの長さは√①②である。①②には一桁の整数が入る。

解答と解説

問４【１】の解答：(√5－√3)/2

分母と分子に(√5－√3)を掛け、分母を有利化します。

(√5－√3)/{(√5＋√3)×(√5－√3)}
＝(√5－√3)/(√5²－√3²)
＝(√5－√3)/(5－3)
＝(√5－√3)/2

問４【２】の解答：AC＝√19

この問題は余弦定理を使って解きます。

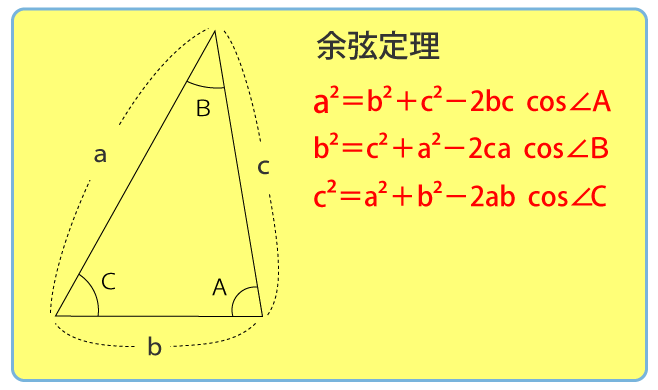
余弦定理より、ACの長さは次の通り。

AC²＝AB²＋BC²－2AB・BC・COS∠B
　＝2²＋5²－2×2×5×COS60°
　＝4＋25－20×1/2
　＝19

AC＝√19

※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。