長崎の職業訓練の試験問題は、本来、全て選択問題ですが下記の問題では選択肢をあえて全て削除しています。試験対策の実施として、自力で解けるようにしておきましょう。
次の各設問の解答を答えなさい。
[問題1]

[問題2]
![]()
[問題3]
6x² + 11xy - 7y² を因数分解しなさい。
[問題4]
1次関数 y = 2x + 1 に並行で点(1,1)を通る1次関数を求めなさい。
[問題5]
不等式 -8 ≦ 3x - 5 ≦ 4 を満たす整数xの値の個数を求めなさい。
[問題6]
![]()
[問題7]
![]()
解答と解説
試験問題1の解答:
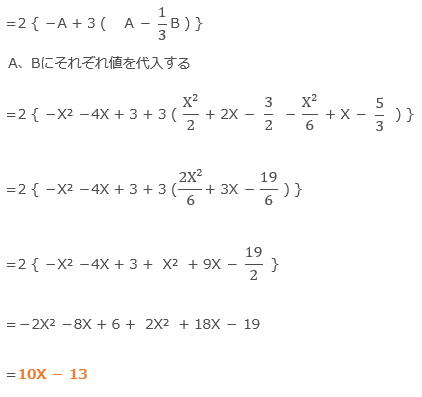
試験問題2の解答:
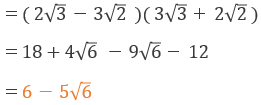
試験問題3の解答:
たすき掛けで因数分解を行う。
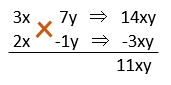
よって、(2x - y)(3x + 7y)
試験問題4の解答:
1次関数y=2x+1の直線と平行ということなので、求めたい1次関数の傾きも2xだとわかる。よって、求めたい1次関数の式は、
y = 2x + b
となる。ここでbの値を求める必要があるのだが、座標 点(1,1)を通るということなので、X=1、Y=1を代入し、bの値を求める。
1 = 2 + b
b = -1
よって、求める1次関数の式は、
y = 2x – 1
となる。
試験問題5の解答:
まずは、不等式 -8 ≦ 3x - 5 に着目して考える。
-8 ≦ 3x - 5
-3 ≦ 3x
-1 ≦ x
xは-1以上だとわかる。
次に、不等式 3x - 5 ≦ 4 に着目して考える。
3x - 5 ≦ 4
3X ≦ 9
X ≦ 3
xは3以下だとわかる。
よって、Xは-1以上3以下となる。設問は、範囲を満たす整数xの値の個数なので、-1、0、1、2、3の計5つがある。
試験問題6の解答:
有利化というのは、平方根をなくすこと。よって、分母を有利化せよということなので、分母から平方根を無くす必要がある。分母の平方根をなくすためには、分母に
![]()
を掛けてやればよい。しかし、分母だけに掛けてしまうと別の数値になってしまうので、必ず分母と分子両方にかけるようにしてください。
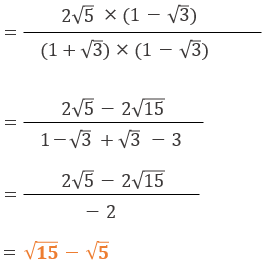
試験問題7の解答:
3x=2y ということなので、y=(3/2)x だとわかる。これを式に代入していく。
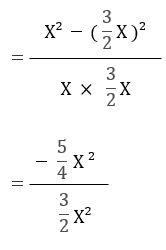
X²は、約分すると分母、分子とも消える。
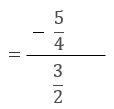
更に分母、分子の両方に2/3を掛けることで、分を無くす。
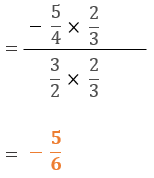


問題3の答えが(2x - y)(3x + 7y)となっていますが、
それならば問題は「6x² + 11xy - y² を因数分解しなさい。」ではなく、「6x² + 11xy - 7y² を因数分解しなさい。」ではないでしょうか?
aaa様
ご指摘ありがとうございます!
問題の記載の方が間違えていました。修正いたしました。
今後ともよろしくお願いします。