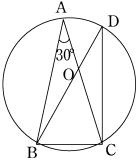
右図のような半径5の円Oに内接する三角形ABC及び、三角形BCDがあり、∠A＝30度とするとき、次の各設問に答えよ。
[問題1]
辺BDが円の中心を通るとき、∠DBCの角度を求めなさい。
①30度 ②45度 ③50度 ④60度
[問題2]
辺BCの長さを求めなさい。
①3 ②4 ③5 ④6
[問題3]
三角形BCDの面積を求めなさい。
[問題4]
常に、cos(180°－θ)＝－cosθ の関係が成り立つ。このことを知って、cos150°の値を求めなさい。
[問題5]
AB＝ACのとき、三角形ABOに着目する。辺AB＝l とするとき、l² を求めなさい。
解答と解説
試験問題１の解答：
三角形ABCと三角形BCDの辺BCが共通の場合は、∠BACと∠BDCは必ず同じになる。よって、∠BDCは、30°だと分かる。更に三角形BCDの辺BDが円の中心を通る場合は、辺BDに向かい合う角は必ず90°となる。よって、∠DCBは、90°となる。
∠BDC＝30°、∠DCB＝90°、三角形の内角の総和は180°なので、残る∠DBCは、60°だと分かる。よって、求める答えは、④。
試験問題２の解答：
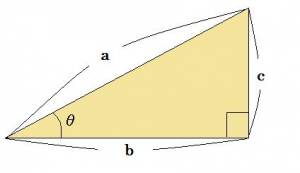三角形BCDは直角三角形なので次の式が利用できる。
cosθ＝b/a
円の中心を通る辺BDは、円の直径になる。円の半径が5なので、辺BDの長さは10とわかる。問題１より、∠DBCは60°なので、辺BCは
cos60°＝b/10
cos60°は、1/2なので、
1/2＝b/10
b＝5
よって、辺BCの長さは5、求める解答は③となる。
試験問題３の解答：
三角形BCDの面積は、辺BCを底辺としたとき高さは辺CDとなる。辺CDの長さは、次の式で表すことができる。
tanθ＝c/b
bは辺BCで問題２より、5だと分かっている。よって、
tan60°＝c/5
なので、
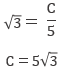
よって、三角形BCDの面積は
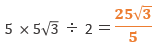
解答は、④
試験問題４の解答：
cos(180°－θ)＝－cosθ の関係が常に成り立つということなので、θ＝30°のとき、
cos(180°－30°)＝－cos30°
cos150°＝－cos30°
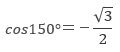
よって、求める解答は、①となる。
試験問題５の解答：
三角形ABOと三角形ABCは辺ABが共通。三角形ABOの頂点Oが円の中心という事は、次の式が成り立つ。
2∠AOB＝∠ACB
∠ACBは、75°なので∠AOBは150だとわかる。
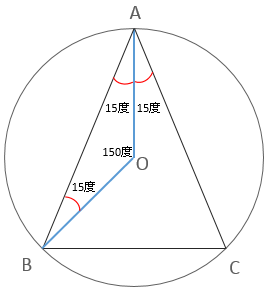
更に、辺AO、辺OBは円の半径なので長さがそれぞれ5だと分かる。辺ABの長さを求める為には下記の余弦定理を使用する。
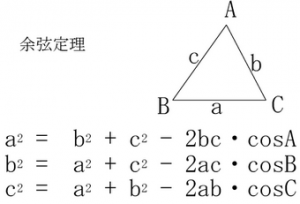
a²＝b²＋c²－2bc・cosA
a＝ℓ、b＝5、c＝5、cosA＝cos150° なので、計算は次のようになる。
ℓ²＝5²＋5²－2x5x5・cos150°
ℓ²＝25＋25－50・cos150°
ℓ²＝50－50・cos150°
問題４より、
とわかっているので、
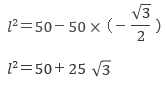
よって、求める解答は④
