長崎 職業訓練 試験問題 数学-問4(平成26年入校生)

次の各設問に答えよ。

[問題1]
赤玉3個と白玉5個の入った袋から、同時に2個の玉を取り出すとき、赤玉と白玉がそれぞれ1個ずつ出る確率を求めよ。

[問題2]
円周上に異なる6個の点がある。これらの点を原点とする三角形は、いくつ作れるか？

[問題3]
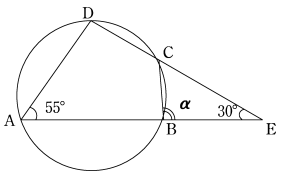右図において、∠αの角度を求めよ。

解答と解説

試験問題１の解答：
赤玉3個と白玉5個の計8個から2個を取り出す場合の総組合せ数は、28通りある。

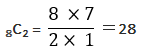
次に、赤玉3個、白玉5個の中から各1個ずつ取り出したいので、その組み合わせ数を求める。

まずは、赤玉3個から1を取り出す組み合わせ数は、3通りだとすぐにわかる。同様に白玉5個から1個を取り出す組み合わせも5通りだとすぐに分かる。

よって、赤玉3個、白玉5個の中から各1個ずつ取り出す組み合わせは、3通り×5通り＝15通り となる。

赤玉3個、白玉5個の中から2個を取り出す総組合せ数28通りの内、赤玉1個、白玉1個を取り出す組合せ数は15通り。したがって、

赤玉3個、白玉5個の中からそれぞれ1個ずつ出る確率は、15/28。

試験問題２の解答：
三角形を作るには3つの点を使用する。よって、6つある頂点の中から3つを選ぶ組み合わせ数を求めればいい。

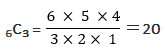
よって、求める解答は、20。

試験問題３の解答：
∠DAE＝55°、∠DEA＝30° なので、∠ADE＝95°だとわかる。

更に円に内接する四角形の向かい合う角の和は180°という性質がある。よって、∠ADEに向かい合う∠CBAは、85°となる。

したがって、求めるαは、

　α＝180°－85°＝95°