平成29年2月17日に大阪で実施された職業訓練の選考試験問題 問4の解説です。大阪で行われる職業訓練の試験問題は、筆記試験ではなく毎回、選択方式ですが試験時間が短いためこれらの過去問を繰り返し実施し、短時間かつ正確に解けるようにしておきましょう。
問1～3に関しては以下のページに解説をまとめているので参考にして下さい。
図は1辺の長さが3の立方体で、Aから辺BC上の点、辺FG上の点を通ってHまでひもをかける。このとき、以下の問いに答えなさい。
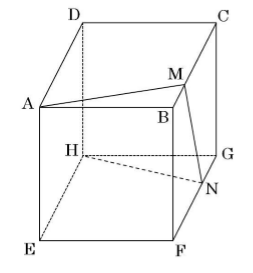
[問題1] 最も短いひもをかけたとき、辺BCの点をM、辺FG上の点をNとすると、AMNHの長さを求めなさい。
[解答群]
ア 2√7 イ 3√10 ウ 4√3 エ 6√13 オ 24
[問題2] 三角形ABM、台形BFNM、台形EFNHの面積の合計を求めなさい。
[解答群]
ア 19/12 イ 39/15 ウ 17/2 エ 27/2 オ 37/10
解答と解説
試験問題１の解答：イ
立方体の展開図を書き、点Aから点Hへまっすぐに直線を引いた線が最短となります。
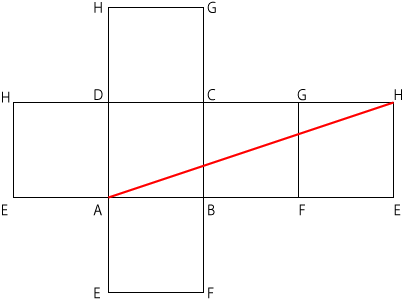
展開図で点Aから点Hへまっすぐに直線を引くと∠HEAを直角とした、直角三角形AHEができあがります。この時、直角三角形AHEの各辺の長さは次の通り。
辺EH＝3
辺AE＝3×3＝9
辺AHの長さは、三平方の定理を用いて求めます。
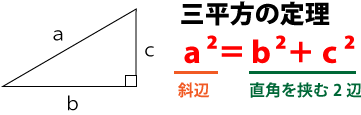
a²＝b²+c²
AH²＝3²＋9²
AH²＝9＋81
AH²＝90
AH＝3√10
よって、求めたい長さは次の通り。
AMNH＝AH＝3√10
試験問題２の解答：エ
三角形ABM、台形BFNM、台形EFNHを合わせた図形は、問題1で解説した直角三角形AHEのことです。よって、この直角三角形AHEの面積を求めればいい。
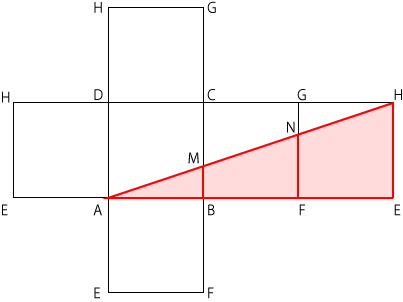
面積＝AExEH÷2
＝9×3÷2
＝27/2
※解説を記載するまでもないと判断した問題に関しては、解説を記載せず解答のみを記載しています。もし、この問題の解説が欲しいというのがあれば、コメント欄に記載してください。また、記載している解説の内容も不明であれば遠慮なくコメントください。
