大阪 職業訓練 試験問題 数学-問2(平成29年8月25日実施) 普通課程

問２ 試験問題

次の文章題の答えとして正しいものをア～オの中から1つ選び、記号で答えなさい。

[問題1]　ある商品の仕入れ値に2割5分の利益を見込んで定価を決めたが、売れないので定価の10%引で値段をつけたら6525円になった。この商品の仕入れ値を求めなさい。

[問題2]　ある美術館の入場料は、1人あたり800円であるが、20人以上の団体の場合、19人を超えた分については、1人あたり600円になる。入場料の総額を団体人数で割って、各人が同じ料金を払うようにする場合、1人あたり700円以下になるのは、何人以上の団体からになるか求めなさい。

[問題3]　兄と弟が1周400ｍの公園の周りを同じ方向に歩いている。今、兄と弟は同じ地点にいて、弟が先に出発してから10分後に、兄が弟を追いかけた。兄は分速60ｍ、弟は分速50ｍのとき、最初に兄が弟に追いつくのは、兄が出発してから何分後になるか求めなさい。

[問題4]　7本のジュ－スをP、Q、Rの3人で分けるとき、その分け方は何通りあるか求めなさい。ただし、3人とも少なくとも1本は受け取るものとする。

[問題5]　ある箱の中には、白玉と赤玉と青玉がそれぞれ3個ずつ入っている。玉を3個同時に取り出したとき、3個とも色が異なる確率を求めなさい。

解答と解説

解答と解説を記載していきます。
解き方が分からないという人を少しでも減らすためにできる限り分かり易く必要以上に細かく順を追って解説している部分がありますが、実際の試験時は丁寧に計算し過ぎると時間のロスに繋がるため、自分の分かるところは効率よく解答していくようにしてください。

問題１の解答と解説

試験問題１の解答：オ

求めたい仕入れ値をＸ円と仮定します。

定価はこの仕入れ値Ｘ円に2割5分を上乗せした金額なので次のように求めることができます。

上乗せ額＝Ｘ×0.25＝0.25Ｘ円

よって、定価は次の通り。

定価＝仕入れ値+上乗せ額
　　＝Ｘ+0.25Ｘ
　　＝1.25Ｘ円

次に低下を10％引きすると6525円になったということなので次の式が成り立ちます。

1.25Ｘ-(1.25Ｘ×0.1)＝6525・・・①
1.125Ｘ＝6525
Ｘ＝5800

よって、仕入れ値は5800円

解き方の補足

式①で『1.25Ｘ-(1.25Ｘ×0.1)＝6525』のように定価から定価の10％を引くといった計算を行いましたが、定価の10％引き後の価格は定価の90％の価格になります。よって、式①は以下のように計算しても構いません。この計算の方がはやいですよね。

1.25Ｘ×0.9＝6525
1.25Ｘ＝7250
Ｘ＝5800

問題２の解答と解説

試験問題２の解答：ア

求めたい団体の人数をＸ人と仮定します。

19人目までの入場料の合計金額は以下の通り。
19×800＝15200円・・・①

20人目からは1人600円になるので20人目以降の入場料合計金額は以下の式で表すことができます。（19人を超えた分なので19人目は該当しないという点に注意。）
(Ｘ-19)×600・・・②

入場料の総額を団体人数で割って、各人の料金が1人あたり700円以下にしたいということなので、以下の式が成り立ちます。

(入場料の総額①+②)/Ｘ≦700

この式を解くと求めたいＸの人数がでてきます。

(入場料の総額①+②)/Ｘ≦700
{15200+(Ｘ-19)×600}/Ｘ≦700
(15200+600Ｘ-11400)≦700Ｘ
15200-11400≦700Ｘ-600Ｘ
3800≦100Ｘ
Ｘ≧38

よって、団体の人数は38人以上であれば1人当たりの入場料が700円以下となります。

問題３の解答と解説

試験問題３の解答：ア

この問題を解くには『速さ、時間、距離を求める公式』を頭に入れておく必要があります。

もし、この公式を忘れてしまった場合、車やバイクのスピードメーターを思い出してください。速度の単位は『ｋｍ/ｈ』ですよね。ｋｍは距離、ｈは時間を表しており、『速度(V)＝距離(ｋｍ)/時間(ｈ)』でまさに上記の公式そのものなのです。

本題に戻りますが、こういった問題は必ず問題用紙の余白などを使って図式化するようにしてください。

弟がスタートする時点は上図のように弟と兄は同じ場所にいるのですが、兄がスタートする10分後は同じ場所にいるとは限りません。よって、まずは兄がスタートするときに弟がどこにいるのかを確認します。

弟が10分間で歩く距離は次の通り。

速度＝距離÷時間
↓
距離＝速度×時間
　　＝50×10
　　＝500ｍ

弟は10分間で500ｍ歩いていることが分かりました。公園1周は400ｍなので、弟は公園を1周回って更に兄がいる位置より100ｍ前にいることになります。

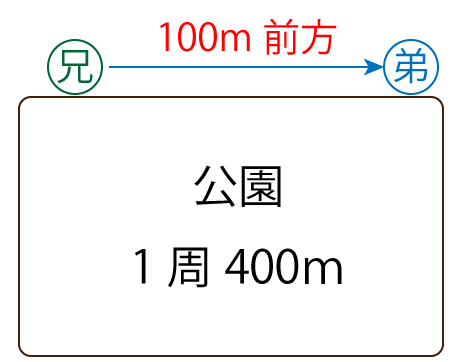
上図の状態から兄がスタートし、弟に追いつくということは以下の式が成り立ちます。

兄の移動距離＝弟の移動距離+100・・・①

求めたい兄がスタートしてから弟に追いつくまでの時間をＸ分と仮定した場合、それぞれの移動距離を求めていきます。

兄の移動距離＝60×Ｘ＝60Ｘ
弟の移動距離＝50×Ｘ＝60Ｘ

これを二人の移動距離を式①に代入すれば求めたい時間Ｘが出てきます。

兄の移動距離＝弟の移動距離+100
60Ｘ＝50Ｘ+100
60Ｘ-50Ｘ＝100
10Ｘ＝100
Ｘ＝10

よって、兄が弟に追いつく時間は兄が出発してから10分後

間違いやすい解答例

これから記載するのはよくやりがちな間違った解答例です。歩く場所が周回ではなく直線であればこの解答で正解なのですが、今回の問題は公園を周回するという点がポイントになります。

求めたい兄が弟に追いつく時間をＸ分と仮定します。

兄が弟に追いつくということは歩いた距離が『兄＝弟』になるということですよね。よって、まずはＸ分後のそれぞれの移動距離を求めます。

速度＝距離÷時間
↓
距離＝速度×時間

兄のＸ分後の移動距離＝60×Ｘ
　　　　　　　　　　＝60Ｘ・・・①

弟は兄よりも10分多く移動しているので移動時間はＸ+10となります。よって、弟の(Ｘ+10)分後の移動距離は次の通り。

弟の(Ｘ+10)分後の移動距離＝50×(Ｘ+10)
　　　　　　　　　　　　　＝50Ｘ+500・・・②

歩いた距離が『兄＝弟』になるので①＝②となります。

60Ｘ＝50Ｘ+500

この式を解くと求めたいＸの値が出てきます。

60Ｘ＝50Ｘ+500
60Ｘ-50Ｘ＝500
10Ｘ＝500
Ｘ＝50

よって、兄が弟に追いつく時間は兄が出発してから50分後

問題４の解答と解説

試験問題４の解答：イ

この問題を解くには組み合わせ数を求める公式を知っている必要があります。

7本のジュースを下図のように横一列に並べて、ジュースとジュースの間に縦棒を2本を任意の場所に入れます。そうすることで、7本のジュースを3等分することができます。

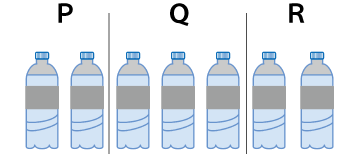
この縦棒2本を入れる場所を変えることで下図のようにPQRに割り当てられる本数が変わってきます。

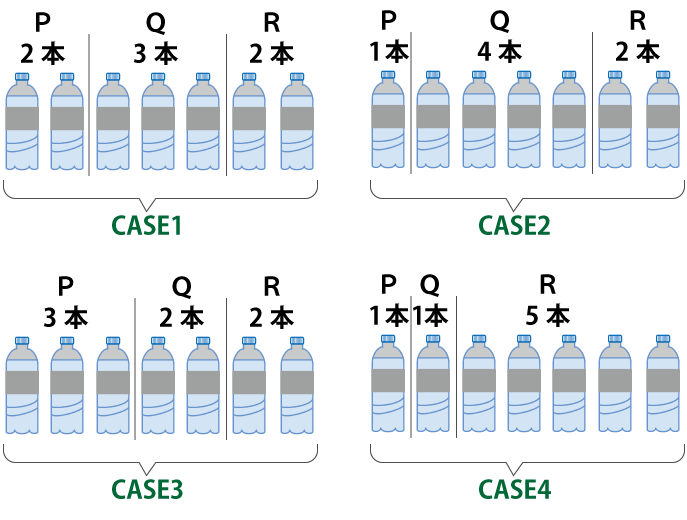
これは、ジュースとジュースの間に縦棒2本を入れる組み合わせ数分だけ、PQR3人のジュースの割りて方があるということを意味します。縦棒を入れられる箇所は以下の6か所があります。

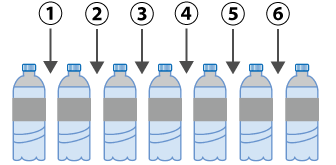
よって、縦棒は6ヵ所から2ヵ所選んで区切るので組み合わせの公式より、組み合わせ数は次の通りになります。

6Ｃ2＝6！/2！(6-2)！
　　＝(6×5×4×3×2×1)/{(2×1)(4×3×2×1)}
　　＝30/2
　　＝15通り

問題５の解答と解説

試験問題５の解答：ウ

3個とも色が異なる確率は以下の式で求まります。

3個とも色が異なる確率＝(3個とも色が異なる組み合わせ数)/(総組み合わせ数)

まず、総組み合わせ数から求めていきます。
全9個の玉の中から3個を取り出す組み合わせ数は次の通り。

9Ｃ3＝9!/3!(9-3)!
　　＝(9×8×7×6×5×4×3×2×1)/{(3×2×1)(6×5×4×3×2×1)}
　　＝504/6
　　＝84

次に3個とも色が異なる組み合わせ数ですが、白玉と青玉と赤玉がそれぞれ3個ずつ入っているので、3個とも色が異なる組み合わせ数は、3×3×3＝27通りになります。

よって、3個とも色が異なる確率は次の通り。

３個とも色が異なる確率＝(3個とも色が異なる組み合わせ数)/(総組み合わせ数)
　　　　　　　　　　　＝27/84
　　　　　　　　　　　＝9/28

※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。