大阪 職業訓練 試験問題 数学-問4(平成29年8月25日実施) 普通課程

問４ 試験問題

下の図のように、台形ABCDがあり、ABを軸として1回転させてできる立体について、以下の問いに答えなさい。ただし、円周率はπとする。

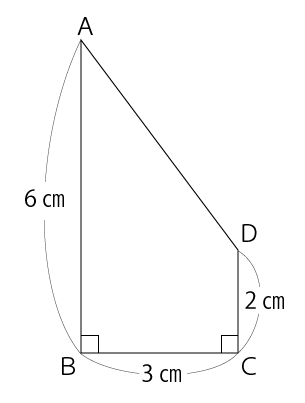
[問題1]　立体の表面積を求めなさい。

[問題2]　立体の体積を求めなさい。

解答と解説

解答と解説を記載していきます。
解き方が分からないという人を少しでも減らすためにできる限り分かり易く必要以上に細かく順を追って解説している部分がありますが、実際の試験時は丁寧に計算し過ぎると時間のロスに繋がるため、自分の分かるところは効率よく解答していくようにしてください。

問題１の解答と解説

試験問題１の解答：ウ

台形ABCDをAB軸に1回点させると下図のような立体になり、この立体の表面積を考える場合、円すいの側面積①、円柱の側面積②、底面の円の面積③の3つに分割して面積を求め、その合計をすることで全体の表面積を求めることができます。

円すいの側面積①

円すい部分のみ抜き出すと下図のようになります。

この円すいの側面積を求める公式は次の通りです。

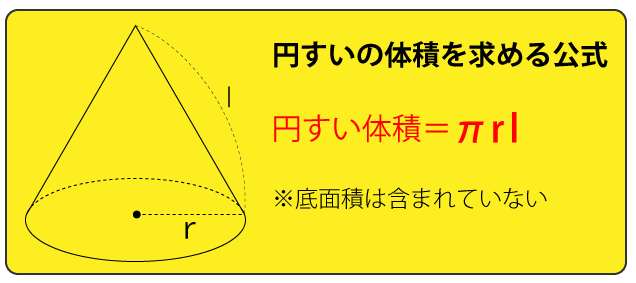
円すいの母線となるADの長さが現時点ではわかっていないのですが、三平方の定理を利用すれば簡単にだすことができます。

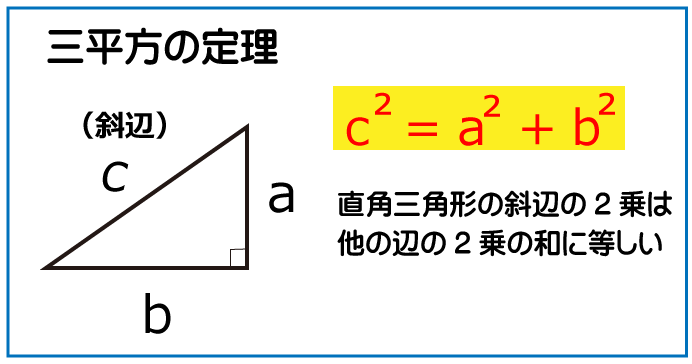
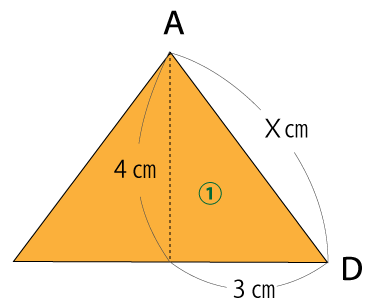
円すい部分は下図なので三平方の定理を利用して母線Ｘを求めていきます。

Ｘ²＝4²+3²
Ｘ²＝16+9
Ｘ²＝25
Ｘ＝5

よって、円すいの側面積は次の通り。

円すいの側面積＝π×3×5
　　　　　　　＝15π・・・①

円柱の側面積

次に円柱部分の側面面積を求めていきます。
円柱部分を抜き出した図と、その円柱の展開図です。

側面積を求めるにはＸの長さを知る必要があります。Ｘの長さは底面の円の円周の長さに等しいので次の通りになります。

Ｘ＝円の直径×π
　＝(3+3)×π
　＝6π

よって、円柱の側面積は次の通り

円柱の側面積＝6π×2＝12π・・・②

底面の円の面積

底面の円は半径3㎝の円なので面積は次の通り。

底面の円の面積＝半径×半径×π
　　　　　　　＝3×3×π
　　　　　　　＝9π・・・③

立体の表面積

最後に台形ABCDをABを軸に1回転してできる立体の表面積を求めます。

これは、これまで求めてきた『円すいの側面積①』、『円柱の側面積②』、『底面の円の面積③』の合計となります。よって、立体の表面積は次の通り。

立体の表面積＝①+②+③
　　　　　　＝15π+12π+9π
　　　　　　＝36π ㎝²

問題２の解答と解説

試験問題２の解答：ア

立体の体積を求めるときも円すい部分と円柱部分に分けて求めていきます。問題１で円すいの母線の長さも分かっているので、円すいと円柱は下図のようになります。

円すいの体積

円すいの体積を求める公式は以下の通り。

既に底面の円の面積は問題１で出しているので『円すいの体積＝Sh/3』を利用した方が計算がらくですよね。

円すいの体積＝Sh/3
　　　　　　＝(9π×4)/3
　　　　　　＝36π/3
　　　　　　＝12π・・・①

円柱の体積

円柱の体積を求める公式は『底面積×高さ』です。

よって、円柱の体積は次の通り。

円柱の体積＝9π×2
　　　　　＝18π・・・②

立体の体積

求めたい立体の体積は既に求めた『円すいの体積②』と『円柱の体積②』を合計したものです。よって、立体の体積は次の通り。

立体の体積＝②+②
　　　　　＝12π+18π
　　　　　＝30π ㎝³

※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。