問1、問3~問4に関しては以下のページに解説をまとめているので参考にして下さい。
大阪 職業訓練 短期過程試験問題 数学-問1
大阪 職業訓練 短期過程試験問題 数学-問3
大阪 職業訓練 短期過程試験問題 数学-問4
次の文章題の答えとして正しいものをア~オの中から1つ選び、記号で答えなさい。
[問題1] 4分で320m歩く人がいる。この人の速さを求めなさい。
[解答群]
ア 時速4km イ 時速4.2km ウ 時速4.4km エ 時速4.6km オ 時速4.8km
[問題2] 兄は分速80m 、弟は分速60mで歩いている。弟の3.6km後ろから兄が弟を追いかけたとすると、兄は弟に何時間後に追いつきますか。
[解答群]
ア 1時間後 イ 2時間後 ウ 3時間後 エ 4時間後 オ 5時間後
[問題3] 1から5のカードを使って3桁の整数をつくる方法は何通りできますか。
[解答群]
ア 6通り イ 24通り ウ 60通り エ 120通り オ 240通り
[問題4] 大小2つのサイコロを同時に投げて出た目の数をx 、yとする。このとき10≦2x+2y≦15となる確率を求めなさい。
[解答群]
ア 5/12 イ 4/9 ウ 17/36 エ 1/2 オ 19/36
[問題5] √350nが自然数となるような自然数nのうち、最も小さいものを求めなさい。
[解答群]
ア 10 イ 14 ウ 15 エ 18 オ 20
解答と解説
試験問題1の解答:オ
———————–
※補足
この問題を解くには下記の速度、時間、距離の関係式を覚えておく必要があります。
速度=距離÷時間
この式が覚えられるか心配な方は車やバイクのスピードメーターの単位を思い出して頂ければ覚えやすいかと思います。スピードメーターには単位として「km/h」と書かれていますよね?これはまさに
速度(km/h)=距離(km)/時間(h)
を表しています。
———————–
この問題を解くにあたり、注意しなければならない点は単位です。問題文は「分」と「m」が使われているのに対し、解答群は「時間」と「km」が使われています。計算前、計算後、どちらでも構わないので単位を統一することを忘れないようにしましょう
下記では計算前に単位を統一しておきます。
4分を時間になおす
4分=4÷60=1/15時間
320mをkmになおす
320m=320÷1000=8/25km
求めたい歩く人の速度は次の通り。
速度=距離÷時間
=(8/25)÷(1/15)
=(8/25)x15
=24/5
=4.8km/h
時速4.8km
試験問題2の解答:ウ
問題1と同様、単位に注意が必要。問題文の中には「分」、「時間」、「m」、「km」が使われているので統一が必要。
ここでは問題を解く前に単位を統一しておきます。
80m/分=80x(1/1000)x60=4.8km/h
60m/分=60x(1/1000)x60=3.6km/h
追いつくまでにかかる時間をHと仮定します。兄が弟に追いつかれるまでに移動した距離をKとした場合、次の式で表すことができます。
速度=距離÷時間
4.8=K÷H
K=4.8H ・・・(1)
次に弟について考えます。弟が兄に追いつかれたとき、弟が移動した距離は兄よりも3.6km少なく、歩いた時間は兄と同じなので次の式で表すことができます。
速度=距離÷時間
3.6=(K-3.6)÷H
K=3.6H+3.6 ・・・(2)
式(1)、式(2)から次の式が成り立ちます。
4.8H=3.6H+3.6
1.2H=3.6
H=3
よって、求める解答は3時間後
試験問題3の解答:ウ
3つの解き方を記載しておきます。
解き方①
5枚から3枚を抜き出し、抜き出した順に1桁目から数字を並べるとします。1桁目にくる数字は5枚から選ばれるので5通りあります。2桁目は1桁目で抜き出された数字を除く4枚の数字から選ばれるので4通りあります。3桁目は同様に3通りとなります。
よって、その組み合わせ数は次の通り。
5x4x3=60通り
解き方②
順列の公式を使います。
n個からr個を取り出して並べる場合、順列の組み合わせ数は次の式で求めることができます。
nPr=n!/(n-r)!
今回は5枚から3枚を選び並べるので次の通りです。
₅P₃=5!/(5-3)!
₅P₃=(5x4x3x2x1)/(2×1)
₅P₃=120/2
₅P₃=60通り
解き方③
組み合わせと、順列の公式を使います。
5枚から3枚を抜き出す組み合わせ数は次の通り。
₅C₃=(5x4x3)/(3x2x1)
₅C₃==60/6
₅C₃=10
3枚から3枚を取り出して並べる順列の組み合わせ数は次の通り。
₃P₃=3!=6
よって、求める順列の組み合わせ数は次の通り。
10×6=60通り
試験問題4の解答:ア
サイコロ2個を投げて出る組み合わせ総数
サイコロ大、サイコロ小ともに出目は6通りなので、総出目は次の通り
6×6=36通り
次に「10≦2x+2y≦15」となる組み合わせ数が何通りあるか求める必要がある。「10≦2x+2y≦15」は以下のように書き換えることができます。
10≦2x+2y≦15
10≦2(x+y)≦15
5≦x+y≦7.5
このことより、サイコロ2個の出た目の和は5、6、7のいずれかだとわかります。出た目の和が5、6、7となるのは下記の15通り。
大 小
1 4
1 5
1 6
2 3
2 4
2 5
3 2
3 3
3 4
4 1
4 2
4 3
5 1
5 2
6 1
よって、確率は次の通り
15/36=5/12
試験問題5の解答:イ
まずは、350を素因数分解すると、次の通りになります。
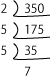
2×5²x7=5²x14
よって、√350nは次のように変形することができます。
√5²x14xn
=5√14n
よって、n=14のとき√内が自然数となる最も小さなnとなります。
※解説を記載するまでもないと判断した問題に関しては、解説を記載せず解答のみを記載しています。もし、この問題の解説が欲しいというのがあれば、コメント欄に記載してください。また、記載している解説の内容も不明であれば遠慮なくコメントください。

