大阪 職業訓練 試験問題 数学-問3(平成28年2月18日実施) 短期課程

図のように2つの放物線ｙ＝ｘ² 、ｙ＝ｘ²/4 とそれに交わる直線ｙ＝4 がある。放物線と直線の交点をA、B、C、Dとするとき、ア～オの中から1つ選び、記号で答えなさい。

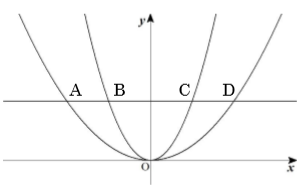
[問題1]　△OCD の面積を求めなさい。

[問題2]　△OADをｘ軸を回転の軸として回転させたときにできる立体の体積を求めなさい。

解答と解説

試験問題１の解答：ウ
——————
※補足
ｙ＝ｘ²とｙ＝ｘ²/4の放物線が2つありますが、図形のどちらのグラフがどちらの式にあたるかは即座に分かるようにしておきましょう。

原点を通る放物線の式は傾きをａとした場合、次の式で表せます。

ｙ＝ａｘ²

グラフの見分け方のポイントは傾きａで、ａの数値が大きい方がグラフの傾きも大きくなります。今回の問題であれば、傾きaは、「1」と「1/4」になり、「1」の方がより傾きが大きいグラフということになります。

問題の図であれば、点BCを通るグラフが「ｙ＝ｘ²」で点ADを通るグラフが「ｙ＝ｘ²/4」となります。

——————

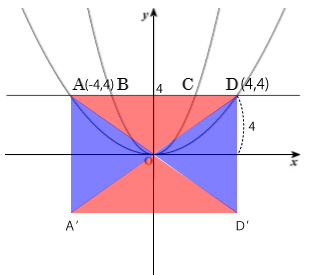
点Cと点Dの座標を求めます。

点Cの座標
点Cは、ｙ＝4のグラフとｙ＝ｘ²のグラフの交点なので、放物線の式にy＝4を代入すればｘの値が求まります。

ｙ＝ｘ²
ｘ²＝4
ｘ＝√4
ｘ＝±2

よって、放物線ｙ＝ｘ²とｙ＝4のグラフが交わる点はｘ＝2とｘ＝－2の2点があることになります。ｘ＝－2は点Bの方にあたるので、点Cのｘ座標は2となります。

点Cの座標(2，4)

点Dの座標
点Aは、ｙ＝4のグラフとｙ＝ｘ²/4のグラフの交点なので、放物線の式にy＝4を代入すればｘの値が求まります。

ｙ＝ｘ²/4
4＝ｘ²/4
ｘ²＝16
ｘ＝√16
ｘ＝±4

よって、放物線ｙ＝ｘ²/4とｙ＝4のグラフが交わる点はｘ＝4とｘ＝－4の2点があることになります。ｘ＝-4は点Aの方にあたるので、点Dのｘ座標は4となります。

点Dの座標(4，4)

△OCDの面積
底辺をCDとした場合、その長さは点Cと点D間のｘ座標の距離となります。点Cのｘ座標は2、点Dのｘ座標は4なのでCD間の距離は次の通り

底辺ACの長さ＝4-2＝2

△OCDの高さは直線ｙ＝4のｙ座標にあたるので、4となります。よって、△OCDの面積は次の通り。

△OAC面積＝底辺ｘ高さ÷2
△OAC面積＝2ｘ4÷2
△OAC面積＝4

試験問題２の解答：エ
△OADをｘ軸を回転の軸として回転させると下図のように横向きに倒れた円柱の青色部分がくり抜かれた図形ができあがります。求められているのはこの青色部分を除いた図形の体積になります。

この問題を解くにあたり、三角錐の体積を求める公式と、円柱の体積を求める公式を頭に入れておく必要があります。

三角錐の体積＝底面積ｘ高さ÷３

円柱の体積＝底面積ｘ高さ

解答までの大まかな流れ

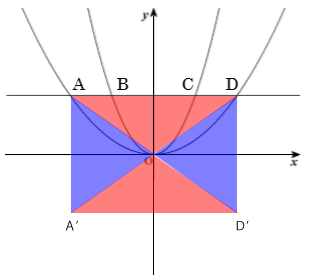
求め方の流れとしては、上図の円柱ADD’A’の体積から三角錐AOA’、三角錐DOD’の体積を引けば赤色部分の図形の体積がでてきます。

円柱ADD’A’の体積
DD’を底面として考えた場合、底面は半径4の円になります。

よって、円柱ADD’A’の底面積は次の通り。

底面積＝4ｘ4ｘπ＝16π

更に円柱の高さは、点Aと点D間の距離なので8だとわかります。よって、円柱の体積を求める公式より、円柱の体積は次の通り。

円柱の体積＝底面積ｘ高さ
　　　　　＝16πｘ8
　　　　　＝128π ・・・(１)

円錐AOA’と円錐DOD’の体積
円錐AOA’と円錐DOD’の体積は同じなので、どちらか一方を求めて2倍すればよい。ここでは、円錐DOD’に着目します。

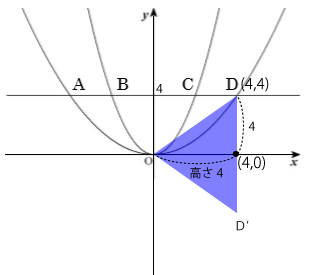
円錐DOD’の底面積は先程求めた円柱の底面積と同じで、半径4の円なので底面積は16π。更に円錐の高さは4なので公式より体積は次の通り。

三角錐の体積＝底面積ｘ高さ÷3
　　　　　　＝16πｘ4÷3
　　　　　　＝64π/3

この三角錐が2個あるので求めた三角錐の体積を2倍します。

64π/3ｘ2＝128π/3

上記の2倍した三角錐の体積を円柱の体積(１)から引けば求めたい図形の体積が求まります。

体積＝128π-128π/3
　　＝384π/3-128π/3
　　＝256π/3

※解説を記載するまでもないと判断した問題に関しては、解説を記載せず解答のみを記載しています。もし、この問題の解説が欲しいというのがあれば、コメント欄に記載してください。また、記載している解説の内容も不明であれば遠慮なくコメントください。