大阪職業訓練試験問題数学-問4(平成28年2月18日実施) 短期課程

平成28年2月18日に大阪で実施された職業訓練の短期過程選考試験問題問4の解説です。大阪で行われる職業訓練の試験問題は、筆記試験ではなく毎回、選択方式ですが試験時間が短いためこれらの過去問を繰り返し実施し、短時間かつ正確に解けるようにしておきましょう。

問1～3に関しては以下のページに解説をまとめているので参考にして下さい。

図のように、平行四辺形ABCDの辺ABを4等分する点のうちAに近い点をE、Bに近い点をFとする。辺CD、DAの中点をそれぞれG、Hとする。またFHとEGの交点をIとし、FHの延長線とCDの延長線の交点をJとする。以下の問いにア～オから選んで答えなさい。

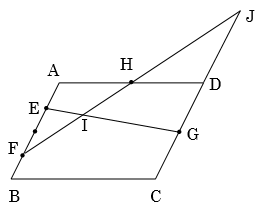
[問題1]　AE：GJを最も簡単な比で表わしなさい。

[解答群]

ア　3：8　　イ　1：3　　ウ　1：5　　エ　3：11　　オ　1：4

[問題2]　EI：IGを最も簡単な比で表わしなさい。

[解答群]

ア　2：3　　イ　1：2　　ウ　3：4　　エ　2：5　　オ　4：5

[問題3]　△EFIの面積を20cm² とするとき、平行四辺形ABCDの面積を求めなさい。

[解答群]

ア　280cm²　　イ　300cm²　　ウ　320cm²　　エ　340cm²　　オ　360cm²

試験問題１の解答：ウ
問題文の条件より下記のことが言えます。
AE＝AB/4 ・・・(１)
GD＝AB/2 ・・・(２)

次に三角形AFHと三角形DJHに着目すると、下記の3点が当てはまり三角形の合同条件の一つでもある「１辺とその両端の角がそれぞれ等しい。」という条件を満たします。よって、この2つの三角形は合同といえます。

１．AH＝DH
２．∠AHF＝∠DHJ
３．∠FAH＝∠JDH

このことより次のことが言えます。

AF＝DJ＝(3/4)ｘAB
DJ＝(3/4)AB ・・・(３)

よって、(１)(２)(３)より次の式が成り立ちます。
AE：GJ＝AE：(GD＋DJ)
AE：GJ＝AB/4：{(AB/2＋(3/4)AB｝
AE：GJ＝AB/4：(5/4)AB
AE：GJ＝AB：5AB
AE：GJ＝1：5

試験問題２の解答：エ
三角形EFIと三角形JGIは、3つの内角が等しいので相似な三角形といえます。その相似比は次の通り。

問題１より、GJ＝(5/4)ABと分かっているのでそれを利用して求めます。

EF：GJ＝EF：(5/4)AB
EF：GJ＝(1/2)AB：(5/4)AB
EF：GJ＝(2/4)AB：(5/4)AB
EF：GJ＝2：5

よって、三角形AFHと三角形DJHの各辺の比率は2:：5なので、下記の点も成り立ちます。

EI：IG＝2：5

試験問題３の解答：ア
三角形EFIと三角形JGIは、3つの内角が等しいので相似な三角形と分かっており(問題1、問題2の解説参照)、その比率は2：5となっています。このことより、点Iから辺ABに垂線を下した長さと、辺CDに垂線を下した長さの比率も2：5となります。

このことより、三角形EFIの辺EFを底面とした場合、三角形EFGの高さは三角形EFIの高さの7/2倍だと言えます。三角形の面積を求める公式は

三角形の面積＝底辺ｘ高さ÷２

であり、底辺は共通のEFなので三角形EFGの面積は次のようになります。

△EFG面積＝△EFI面積ｘ7/2
△EFG面積＝20ｘ7/2
△EFG面積＝70

次に三角形委ABGについて考えます。三角形ABGは三角形EFGと高さが同じ。底面の長さが2倍あるので△ABGの面積は次の通りになります。

△ABG面積＝△EFG面積ｘ2
△ABG面積＝70ｘ2
△ABG面積＝140

また、△ABGの面積は平行四辺形ABCDを丁度2等分した大きさになります。
△ABG＝△AGD＋△BGC

よって、平行四辺形ABCDの面積は次の通り。

140ｘ2＝280 ㎝²

※解説を記載するまでもないと判断した問題に関しては、解説を記載せず解答のみを記載しています。もし、この問題の解説が欲しいというのがあれば、コメント欄に記載してください。また、記載している解説の内容も不明であれば遠慮なくコメントください。

関連記事