大阪職業訓練試験問題数学-問4(平成28年2月19日実施) 短期課程

平成28年2月19日に大阪で実施された職業訓練の短期過程選考試験問題問4の解説です。大阪で行われる職業訓練の試験問題は、筆記試験ではなく毎回、選択方式ですが試験時間が短いためこれらの過去問を繰り返し実施し、短時間かつ正確に解けるようにしておきましょう。

問1～3に関しては以下のページに解説をまとめているので参考にして下さい。

図のように、1辺が10cmの正方形があり、その正方形から高さａcmの二等辺三角形を4つ切り取ると、正四角すいの展開図ができる。正四角すいの表面積が50cm²であるとき、以下の問いにア～オから選んで答えなさい。

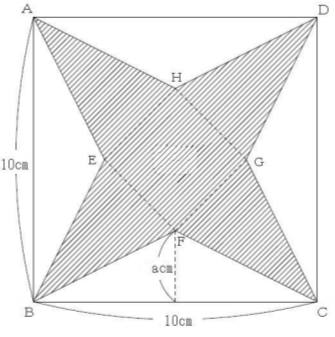
[問題1]　ａの値を求めなさい。

[解答群]

ア　5　　イ　5√2　　ウ　5√2/2　　エ　5/2　　オ　3/10

[問題2]　△AEH、△BFE、△CGF、△DHGの4つの三角形の面積の合計を求めなさい。

[解答群]

ア　75/2 cm²　　イ　25 cm²　　ウ　30√2 cm²　　エ　25/2 cm²　　オ　50/3 cm²

試験問題１の解答：エ
正四角推の表面積は次の式で表すことができます。

正四角推の表面積＝正方形の面積-二等辺三角形の面積x4

正方形の面積を求める
一辺が10cmの正方形なので面積は次の通り。

10ｘ10＝100cm²

二等辺三角形の面積
底辺の長さが10cm、高さがａcmなので二等辺三角形4つの面積は次の通り。

　(10ｘａ÷2)ｘ4
＝20ａ

高さａを求める
正四角推の表面積は50cm²なので次の式で高さａを求めることができます。

正四角推の表面積＝正方形の面積-二等辺三角形の面積x4
50＝100-20ａ
20ａ＝100-50
20ａ＝50
ａ＝50/20＝5/2

試験問題２の解答：ア
問題１より、ａの長さが5/2と分かっているので、下図のＨＦ間の距離は5㎝だとわかります。

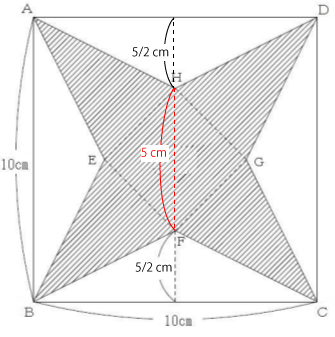
このことより、正方形ＨＥＦＧの面積は次のように求めることができます。

正四角形ＨＥＦＧは、下図の様に底辺が5/2㎝、高さが5/2㎝の直角三角形4つに分けることができます。

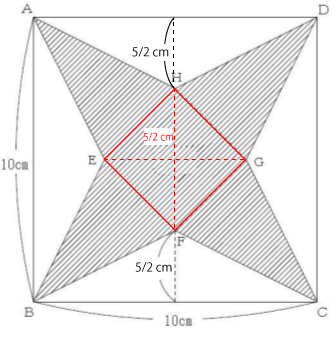
よって、正四角形ＨＥＦＧの面積は次の通り。
　(5/2ｘ5/2÷2)ｘ4
＝25/2 cm²

正四角推の表面積から上記の正四角形の面積を引けば、△AEH、△BFE、△CGF、△DHGの4つの三角形の面積の合計がでてきます。

50-25/2＝75/2 cm²

※解説を記載するまでもないと判断した問題に関しては、解説を記載せず解答のみを記載しています。もし、この問題の解説が欲しいというのがあれば、コメント欄に記載してください。また、記載している解説の内容も不明であれば遠慮なくコメントください。

関連記事