大阪 職業訓練 試験問題 数学-問3(平成28年8月26日実施) 短期課程

ｙ＝ｘ²/4上の2点A、Bのx座標をそれぞれ－2、4とする。2点A、Bを通る直線ℓのx軸、ｙ軸との交点をそれぞれC、Dとする。以下の問いにア～オから選んで答えなさい。

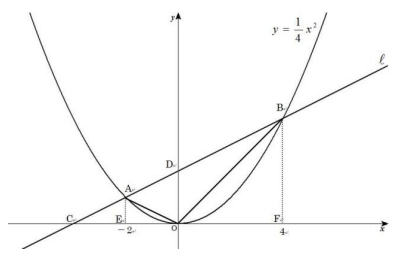
[問題1]　点Dの座標を求めなさい。

[問題2]　台形AEFBの面積を求めなさい。

解答と解説

試験問題１の解答：ア
点A、点Bの座標を求める。

点A、点Bのｘ座標がそれぞれ-2、4というのは分かっているので、放物線ｙ＝ｘ²/4に値を代入し、ｙ座標も求めます。

点Aの座標
ｙ＝ｘ²/4
　＝(-2)²/4
　＝1

点A(-2,1)

点Bの座標
ｙ＝ｘ²/4
　＝4²/4
　＝4

点B(4,4)

直線ℓの式を求める
傾きをａ、ｙ軸との交点である切片をｂとした場合、直線ℓの式は次の式で表すことができます。

ｙ＝ａｘ+ｂ

この直線は点Ａと点Ｂを通るので、それぞれの値を代入し、ａとｂの値を求めます。

点A(-2,1)を通ることより、次のことが言える

1＝-2ａ+ｂ ・・・(１)

点B(4,4)を通ることより、次のことが言える

4＝4ａ+ｂ ・・・(２)

(２)-(１)ｘ2をする

4＝4ａ+ｂ ・・・(２)
2＝-4ａ+2ｂ ・・・(１)
————————
6＝3ｂ
ｂ＝2

ｙ軸との交点である切片ｂの値が2と分かったので、点Ｄの座標は次の通り。

点Ｄ(0,2)

試験問題２の解答：オ
台形の面積を求める公式は次の通り。

台形面積＝(上底+下底)ｘ高さ÷２

ここでは、上底をＡＥ、下底をＢＦ、高さをＥＦとすると、各座標より、それぞれの長さは次の通り。

ＡＥ＝1
ＢＦ＝4
ＥＦ＝6

台形面積＝(上底+下底)ｘ高さ÷２
　　　　＝(1+4)ｘ6÷2
　　　　＝15

※解説を記載するまでもないと判断した問題に関しては、解説を記載せず解答のみを記載しています。もし、この問題の解説が欲しいというのがあれば、コメント欄に記載してください。また、記載している解説の内容も不明であれば遠慮なくコメントください。