問1、問3~問4に関しては以下のページに解説をまとめているので参考にして下さい。
大阪 職業訓練 短期過程試験問題 数学-問1
大阪 職業訓練 短期過程試験問題 数学-問3
大阪 職業訓練 短期過程試験問題 数学-問4
次の文章題の答えとして正しいものをア~オの中から1つ選び、記号で答えなさい。
[問題1] 54の正の約数の総和を求めなさい。
[解答群]
ア 66
イ 93
ウ 102
エ 114
オ 120
[問題2] 図の∠xの大きさを求めなさい。
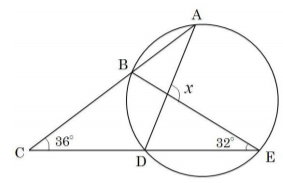
[解答群]
ア 98° イ 100° ウ 102° エ 104° オ 110°
[問題3] 同じ値段のペンを12本買うには、持っているお金では200円足りず、8本買うと400円余る。ペン1本の値段を求めなさい。
[解答群]
ア 90円 イ 100円 ウ 120円 エ 130円 オ 150円
[問題4] 濃度7%の食塩水200gとある濃度の食塩水300gを混ぜたら、濃度4%の食塩水になった。食塩水300gの濃度を求めなさい。
[解答群]
ア 1% イ 1.5% ウ 2% エ 2.5% オ 3%
[問題5] 家から16km離れた駅に行くのに、はじめは時速12kmで走り、途中から時速4kmで歩いた。家から駅まで2時間30分かかったとき、歩いた距離を求めなさい。
[解答群]
ア 2km イ 4km ウ 5km エ 7km オ 10km
解答と解説
試験問題1の解答:オ
54の約数={1,2,3,6,9,18,27,54}
計算が得意な人はそのまま足し算をすればよいが、苦手な人は下記のように計算すれば若干簡単になります。
総和=1+2+3+6+9+18+27+54
=(1+9)+(2+18)+(3+27)+(6+54)
=10+20+30+60
=120
試験問題2の解答:イ
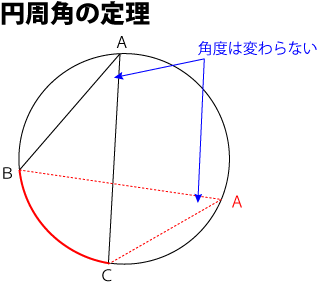
この問題を解くには「円周角の定理」を知っておく必要があります。
円周角の定理とは、下図の様に円周上の弧BCが一定の場合、点Aを円周上のいかなる場所に移動しても∠BACは変わらないというもの。
分かるところから角度を確認していきます。ここでは、下図の順番に角度を求めていきます。
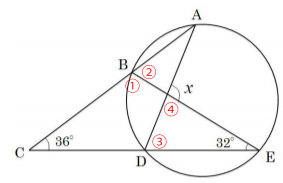
①の角度
三角形の内角の和は180°なので、①の角度は次の通り。
①の角度=180-36-32=112°
②の角度
②の角度=180-112=68°
③の角度
円周角の定理より、②と③の角度は等しいので、③の角度は68°
④の角度
④の角度=180-68-32=80°
xの角度
xの角度=180-80=100°
試験問題3の解答:オ
持っているお金をM、求めたいペン1本の値段をN円と仮定します。
12本買うと200円不足するので次の式が成り立ちます。
12xN=M+200
12N=M+200 ・・・(1)
8本買うと400円余るという点から次の式が成り立ちます。
8xN=M-400
8N=M-400 ・・・(2)
(1)-(2)をすれば、Nの値が求まります。
12N=M+200 ・・・(1)
8N=M-400 ・・・(2)
——————–
4N=600
N=150円
試験問題4の解答:ウ
この問題を解くには、食塩水の量、食塩の量、食塩水の濃度の関係式を覚えておく必要があります。
食塩水の濃度=食塩の量÷食塩水の量
元々の食塩水に含まれる食塩の量を求める
濃度7%
食塩水200g
食塩水の濃度=食塩の量÷食塩水の量
0.07=食塩の量÷200
食塩の量=14g
よって、元々の食塩水の内容は次の通り。
濃度7%
食塩水200g
食塩の量14g
この食塩水に別の濃度の食塩水300gを加えたら濃度が4%に薄まったということなので、次の式が成り立ちます。注意点としては、食塩水を加えるのでそこに含まれる食塩のことも考慮すること。ここでは、後から加えて食塩水300gに含まれている食塩の量をMグラムと仮定します。
食塩水の濃度=食塩の量÷食塩水の量
0.04=(14+M)÷(200+300)
0.04=(14+M)÷500
14+M=20
M=6g
後から加えた食塩水は、食塩水の量が300g、含まれる食塩の量が6gと分かったので、濃度は次の通り。
食塩水の濃度=食塩の量÷食塩水の量
=6÷300
=0.02
=2%
試験問題5の解答:エ
この問題を解くにあたり知っておかなければならないのが、速度、距離、時間の関係式です。
速度=距離÷時間
問われている内容を図に落とし込むと下図の通り。
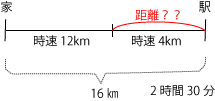
求めたい歩いた距離をMと仮定した場合、走った距離は16-Mと表すことができます。また、歩いた時間と走った時間を足すと2時間30分となるので、次の式が成り立ちます。
2時間30分=2.5時間
「速度=距離÷時間」
この公式を書き換えると次のように変形できます。
時間=距離÷速度
歩いた時間
歩いた時間=M/4
走った時間
走った時間=(16-M)/12
トータル時間
2.5=歩いた時間+走った時間
2.5=(M/4)+{(16-M)/12}
2.5=(3M+16-M)/12
30=3M+16-M
2M=14
M=7km
※解説を記載するまでもないと判断した問題に関しては、解説を記載せず解答のみを記載しています。もし、この問題の解説が欲しいというのがあれば、コメント欄に記載してください。また、記載している解説の内容も不明であれば遠慮なくコメントください。

