大阪職業訓練試験問題数学-問3(平成29年2月17日実施) 短期課程

平成29年2月17日に大阪で実施された職業訓練の短期過程選考試験問題問3の解説です。大阪で行われる職業訓練の試験問題は、筆記試験ではなく毎回、選択方式ですが試験時間が短いためこれらの過去問を繰り返し実施し、短時間かつ正確に解けるようにしておきましょう。

問1～2、問4に関しては以下のページに解説をまとめているので参考にして下さい。

座標平面上にA（－4,3）、B（－2,－3）、C（4,－1）があり、各点を結び三角形ABCを作る。以下の問いにア～オから選んで答えなさい。ただし、座標軸の1目盛りを1cmとする。

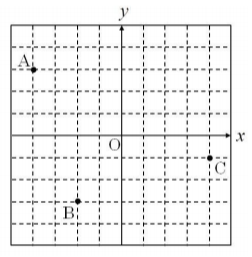
[問題1]　辺ABの長さを求めなさい。

[解答群]

ア　6 cm　　イ　2√5 cm　　ウ　8√5 cm　　エ　2√10 cm　　オ　4√10 cm

[問題2]　∠BACの大きさを求めなさい。

[解答群]

ア　30°　　イ　45°　　ウ　60°　　エ　75°　　オ　90°

[問題3]　△ABC の面積を求めなさい。

[解答群]

ア　20 cm²　　イ　10√5 cm²　　ウ　20√2 cm²　　エ　40 cm²　　オ　80 cm²

試験問題１の解答：エ
この問題を解くには三平方の定理を頭に入れておく必要がある。

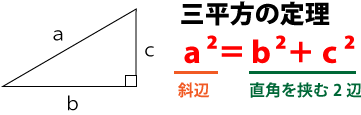
下図の様な直角三角形で考える。

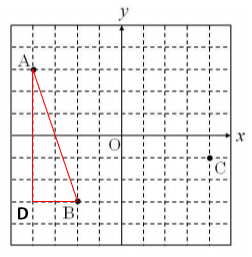
1メモリが1cmなので、ADの長さは6cm。BDの長さは2cm。三平方の定理よりABの長さは次の通り。

AB²＝AD²+BD²
AB²＝6²+2²
AB²＝36+4
AB²＝40
AB＝2√10 cm

試験問題２の解答：イ
問題1と同様に辺BCの長さを求めると辺ABと同じ長さだとすぐに分かります。ここで気付いて欲しいのが、下図の様に三角形ABDと三角形BCEは全く等しい三角形だという点です。

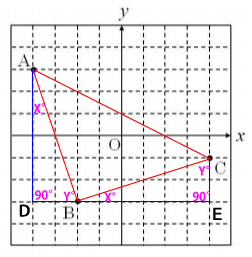
このことより、辺ABと辺BCの長さは等しいことがわかります。更にＸ°+Ｙ°＝90°なので、∠ABC＝90°というのもわかります。よって、三角形ABCは頂点Bが直角の直角二等辺三角形ということになります。

直角二等辺三角形の直角以外の2角はそれぞれ、45°なので求めたい∠BACも45°となります。

試験問題３の解答：ア
AB＝BC＝2√10 cm

BCを底辺とした場合、三角形ABCの面積は次の通り。

△ABCの面積＝2√10x2√10÷2
△ABCの面積＝20 cm²

※解説を記載するまでもないと判断した問題に関しては、解説を記載せず解答のみを記載しています。もし、この問題の解説が欲しいというのがあれば、コメント欄に記載してください。また、記載している解説の内容も不明であれば遠慮なくコメントください。

関連記事