大阪 職業訓練 試験問題 数学-問4(平成29年2月17日実施) 短期課程

図は底面の半径が6cm、母線の長さが10cmの円すいである。以下の問いにア～オから選んで答えなさい。ただし、円周率はπとする。

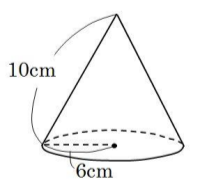
[問題1]　円すいの表面積を求めなさい。

[問題2]　円すいの体積を求めなさい。

解答と解説

試験問題１の解答：オ
円錐を展開すると下図の様に扇型と円の2つの図形から成り立っています。円錐の表面積は、この扇型の面積と円の面積を求めればよい。

円の面積を求める
半径6cmの円なので面積は次の通り。

円の面積＝6x6xπ＝36π

扇型の面積を求める
扇型の面積を求める前に扇型の弧の長さを求めます。扇型の弧の長さは半径6cmの円の円周の長さに等しいので、その長さは次の通り。

弧の長さ＝(6+6)xπ＝12π

次に半径10cmの円の円周を求めます。

半径10cmの円の円周＝(10+10)xπ＝20π

このことより、扇型の大きさは半径10cmの円を12π/20π＝3/5にした大きさだとわかります。よって、面積も半径10cmの円の3/5になります。

半径10cmの円の面積＝10x10xπ＝100π

扇型の面積＝100πx3/5
　　　　　＝60π

よって、扇型の面積は次の通り。

扇型の面積＝36π+60π
　　　　　＝96π cm²

試験問題２の解答：ウ
円錐の体積を求める公式は次の通り。

円錐の体積＝底面積ｘ高さ÷３

底面となる半径6cmの円の面積は既に求めているので、高さがわかれば円錐の体積を求めることができます。ここで、高さを求めるには三平方の定理を知っている必要があります。

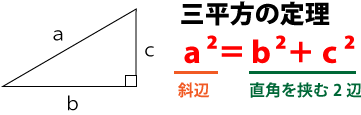
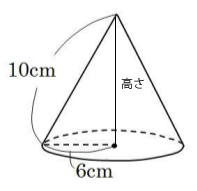
三平方の定理より高さは次の通り。

10²＝6²+(高さ)²
100＝36+(高さ)²
(高さ)²＝64
高さ＝√64
　　＝8

よって、円錐の体積は次の通り。

円錐の体積＝底面積ｘ高さ÷３
　　　　　＝36πx8÷3
　　　　　＝96π cm³

※解説を記載するまでもないと判断した問題に関しては、解説を記載せず解答のみを記載しています。もし、この問題の解説が欲しいというのがあれば、コメント欄に記載してください。また、記載している解説の内容も不明であれば遠慮なくコメントください。