埼玉 職業訓練 試験問題[長期] 数学-問2(平成27年入校生)

平成27年度に埼玉県で実施された職業訓練の選考試験で出題された試験問題と、その解答と解説です。 本ページでは数学問題の設問2(正式なテスト用紙上では設問5)のみ記載しています。数学問題の設問1、3に関しては、以下のページを参照してください。

埼玉 職業訓練 試験問題[長期] 数学-問1(平成27年入校生)
埼玉 職業訓練 試験問題[長期] 数学-問3(平成27年入校生)

試験問題 設問２

次の（１）～（４）の問いに答えなさい。

[問題1]
面積が１５cm²で、横が縦より２cm長い長方形がある。この長方形の縦の長さを求めなさい。

[問題2]
原価に２割の利益を見込んで定価をつけ、定価の２００円引きで売ったら、３００円の利益があった。原価を求めなさい。

[問題3]
りんご３個となし２個を買うと５２０円で、りんご２個となし１個を買うと３２０円だった。りんご１個、なし１個の値段をそれぞれ求めなさい。

[問題4]
Ａ君の家から公園を通って駅まで行くと１,０００ｍある。Ａ君が家を出てから公園まで毎分８０ｍで歩き、公園から駅までは毎分５０ｍで歩くと家から駅まで１４分かかった。家から公園までは何ｍか求めなさい。

解答と解説

試験問題１の解答：
長方形の縦の長さをＸとします。長方形の横の長さは縦の長さよりも２cm長いので横の長さはＸ+２となります。

縦の長さ　Ｘ
横の長さ　Ｘ+２

長方形の面積を求める式は、縦×横。設問より面積は１５cm²と分かっているので次の式で表すことができます。

Ｘｘ（Ｘ+２）＝１５

この式を解くと縦の長さＸが求まります。

Ｘｘ（Ｘ+２）＝１５
Ｘ²+２Ｘ＝１５
Ｘ²+２Ｘ-１５＝０
(Ｘ+５)(Ｘ-３)＝０

よって、Ｘ＝-５、３

辺の長さにマイナスはあり得ないので、縦の長さは３cmとなります。横の長さは縦の長さよりも２cm長いので５cmとなります。

よって、求める解答は

縦の長さ３cm

※補足
この程度の問題の場合、二次方程式にして計算するよりも一片の長さがＸでもう一辺がＸ+２、そして面積が１５cmであれば頭の中で即、一片の長さが３cmと５cmと思い浮かべられるようにしたいところです。

解答：３cm

試験問題２の解答：
原価に２割の利益を見込んで定価を付けるということは、原価に原価の２割の額を上乗せするということになり、次のことを意味します。

定価で売った場合
利益＝原価x０.２　・・・（１）

更に、設問の「定価の２００円引きで売ったら、３００円の利益があった。」という点より、２００円引きで売らず定価で売った場合、利益が５００円（２００円+３００円）だと分かります。これを（１）式にあてはめると次の式になります。

利益＝原価x０.２　・・・（１）
５００円＝原価x０.２

この式を解くと求めたい原価がでてきます。

５００円＝原価x０.２
原価＝５００÷０.２
　　＝２５００円

解答：２５００円

試験問題３の解答：
求めたいりんご1個の値段をＸ、なし1個の値段をＹとします。

設問の「りんご3個となし2個を買うと520円」という点より以下の式が成り立ちます。
3Ｘ+2Ｙ＝520 ・・・(１)

更に「りんご2個となし1個を買うと320円」という点より以下の式が成り立ちます。
2Ｘ+Ｙ＝320 ・・・(２)

この式(１)と(２)の連立方程式を解くと求めたいＸとＹの値がでてきます。
3Ｘ+2Ｙ＝520 ・・・(１)
2Ｘ+Ｙ＝320 ・・・(２)

式(２)の両辺に2を掛けます。
2Ｘx2+Ｙx2＝320×2 ・・・(２)
4Ｘ+2Ｙ＝640 ・・・(２)

式(２)－式(１)をすればＸの値が求まります。
4Ｘ+2Ｙ＝640 ・・・(２)
3Ｘ+2Ｙ＝520 ・・・(１)
————————
Ｘ＝120

更にこの「Ｘ＝120」を式(１)もしくは式(２)に代入するとＹの値も求まります。
2Ｘ+Ｙ＝320 ・・・(２)
2×120+Ｙ＝320
240+Ｙ＝320
Ｙ＝320-240
Ｙ＝80

よって、りんご1個の値段は120円、なし1個の値段は80円となります。

解答：りんご120円、なし80円

試験問題４の解答：

こういった問題は下図のように図にした方が間違え難く、解くのも容易になることが多いです。

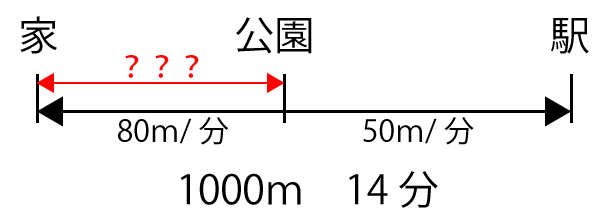
求めたい家から公園までの距離をＸとします。そうすると、公園から駅までの距離は次の様に表すことができます。

家から公園までの距離：Ｘ
公園から駅までの距離：1000-Ｘ

公式を使って家から公園までにかかった時間と、公園から駅までにかかった時間は次の様に表すことができます。

家から公園までにかかった時間
時速＝距離÷時間
80＝Ｘ÷時間
時間＝Ｘ/80 ・・・(１)

公園から駅までにかかった時間
時速＝距離÷時間
50＝(1000-Ｘ)÷時間
時間＝(1000-Ｘ)/50 ・・・(２)

設問より、家から公園まで歩くのにかかった時間は１４分だと分かっています。よって、式(１)と式(２)の合計時間が１４分ということになります。

(１)+(２)＝１４分
(Ｘ/８０)+{(１０００-Ｘ)/５０}＝１４

この式を解くと求めたい距離Ｘがでてきます。解き方はいくつかありますが、分数計算は面倒なので私であれば両辺に４０００を掛けて整数計算にします。

(Ｘ/80)x4000+{(1000-Ｘ)/50}x4000＝14×4000
50Ｘ+(1000-Ｘ)x80＝56000
50Ｘ+80000-80Ｘ＝56000
50Ｘ-80Ｘ＝56000-80000
-30Ｘ＝-24000
Ｘ＝800

よって、家から公園までの距離は８００ｍ

解答：８００ｍ