平成27年度に埼玉県で実施された職業訓練の選考試験で出題された試験問題と、その解答と解説です。 本ページでは数学問題の設問3(正式なテスト用紙上では設問6)のみ記載しています。数学問題の設問1~2に関しては、以下のページを参照してください。
埼玉 職業訓練 試験問題[長期] 数学-問1(平成27年入校生)
埼玉 職業訓練 試験問題[長期] 数学-問2(平成27年入校生)
試験問題 設問3
AB=15cm、AC=10cmの三角形がある。下図のように、頂点Cから辺ABに垂線CDを引く。AD=6cmのとき、三角形ABCの面積を求めなさい。
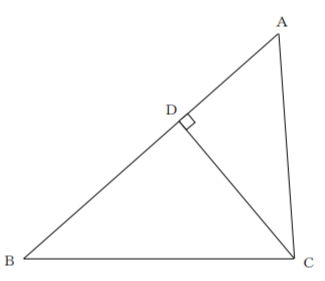
解答と解説
設問の内容から分かっている数値を図に書き込むと下図のようになります。
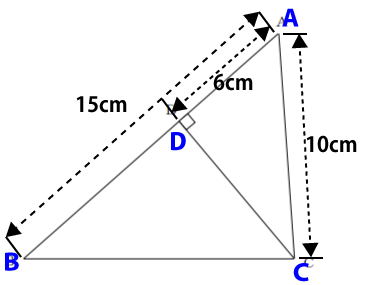
三角形ABCの面積を求める場合、辺ABを底辺、垂線CDを高さとすると次の式で求めることができます。
三角形ABCの面積=(辺AB)x(垂線CD)÷2
辺ABは設問より15cmと分かっているので、垂線CDの長さが分かれば三角形ABCの面積を求めることができます。垂線CDの長さを求めるには三角形ACDに着目します。三角形ACDは直角三角形で直角三角形の場合、各辺の長さは次の式が成り立ちます。(これを三平方の定理と言う)
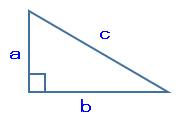
a²+b²=c²
この式は覚えておくようにしましょう。
求めたい辺CDの長さをXとし、この式を三角形ACDにあてはめると次の様になります。
a²+b²=c²
6²+X²=10²
36+X²=100
X²=100-36
X²=64
X=8cm
これで辺CDの長さが8cmと分かりました。よって、三角形ABCの面積は次の通りになります。
三角形ABCの面積=底辺×高さ÷2
=15×8÷2
=60cm²
よって、三角形ABCの面積は、60cm²
解答:60cm²

