埼玉 職業訓練 試験問題[短期] 数学-問8(令和元年度入校生)

問８ 試験問題

次の（１）、（２）の問いに答えなさい。

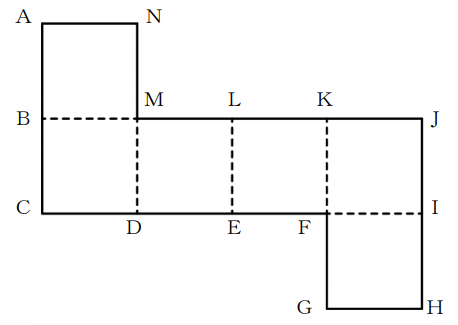
（１）下図は立方体の展開図である。この展開図を組み立ててできる立方体について、頂点Ａと重なる点を下図のＢからＮより選び答えなさい。

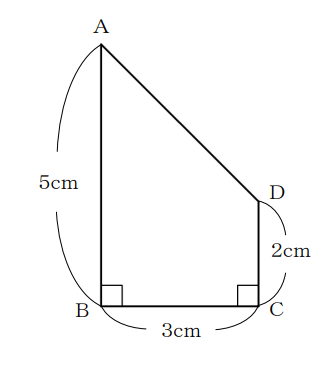
（２）下の図のような台形ＡＢＣＤがある。この台形を辺ＡＢを軸として１回転させてできる立体の体積を求めなさい。ただし、円周率はπとする。

※以下は解答と解説ですが、見る前にまずは、自分自身でしっかりと解いてみてください。

解答と解説

解答と解説を記載していきます。
解き方が分からないという人を少しでも減らすためにできる限り分かり易く必要以上に細かく順を追って解説している部分がありますが、実際の試験時は丁寧に計算し過ぎると時間のロスに繋がるため、自分の分かるところは効率よく解答していくようにしてください。

問題１の解答と解説

試験問題（１）の解答：Ｋ

この問題は、図形を組み立てたときの図形をいかにイメージできるかだけを問われている問題なので、特に効果的な解き方というのは存在しませんが、ちょっとしたコツだけを紹介しておきます。

展開図からなんとなくサイコロ型の正立方体になることは想像つきますよね？
問題は頂点Ａとくっつく他の頂点を見つけろということですが、くっつく頂点がイメージし難い原因は実は四角形ＦＧＨＩにあります。もし、四角形ＦＧＨＩを下図のようにＣＧＨＤに移動したらどうでしょうか？

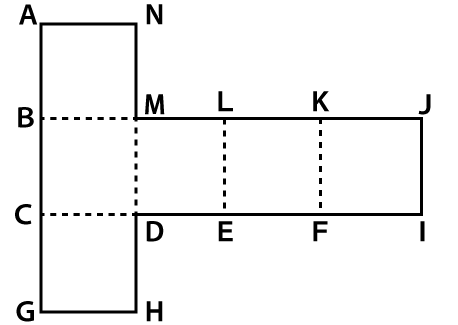
この展開図も組み立てると全く同じ正立方体になります。頂点Ａは、勘のいい人であれば四角形ＦＧＨＩのどの部分にもくっつかないというのがすぐにわかると思います。よって、上図のようにＣＧＨＤに移動しても影響はありません。

このように展開図を変形することで頂点Ａがどこにくっつくのかイメージしやすくなったと思います。頂点Ｎは頂点Ｌと、頂点Ａは頂点Ｋと、頂点Ｂは頂点Ｊとくっつきます。

よって、頂点Ａは頂点Ｋと重なります。

※当たり前ですが、全く違う形になる展開図に変形はしないようにしてくださいね。変形させる場合は、必ず組み立てたとき同じ図形になるようにする必要があります。

問題２の解答と解説

試験問題（２）の解答：27π cm³

問題の図形を辺ＡＢを軸にして回転させると下図のような図形になります。

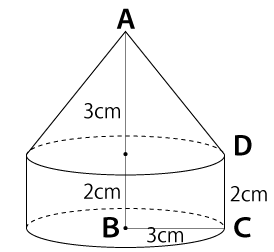
この図形は、円柱部分と三角錐の図形部分に分かれることが見て分かると思います。よって、体積もこの円柱と三角錐わけてそれぞれ求めていきます。

円柱の体積

円柱の体積を求める公式は次の通り。

円柱の体積＝底面積×高さ

底面は半径3cmの円なので面積は次の通り。
底面積＝半径×半径×π
　　　＝3×3××π
　　　＝9π

高さは2cmなので円柱の体積は次の通り。
円柱の体積＝底面積×高さ
　　　　　＝9π×2
　　　　　＝18π cm³

三角錐の体積

三角錐の体積を求める公式は次の通り。

底面積は、先程求めた円柱の底面積と同じなので9πだとすぐにわかります。また、三角錐の高さは5cm－2cm＝3cm です。よって、三角錐の体積は次の通り。

三角錐の体積＝底面積×高さ×13
　　　　　　＝9π×3×13
　　　　　　＝9π cm³

求めたい図形の体積

求めたい図形の体積は円柱と三角錐の体積の合計なので次のようになります。

求めたい図形の体積＝18π＋9π
　　　　　　　　　＝27π cm³

※解説を記載するまでもないと判断した問題に関しては、解説を記載せず解答のみを記載しています。もし、この問題の解説が欲しいというのがあれば、コメント欄に記載してください。また、記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。