この問題は令和元年（平成31年）度入校の埼玉県立技術専門校 求職者対象（短期コース）入校試験問題の問９(問１～５は国語)の解答と解説です。

問6～問8に関しては以下のページに解説をまとめているので参考にして下さい。

実際の試験の問題用紙は以下のページで確認することができます。

⇒令和元年度入校生 埼玉県立高等技術専門校短期コース 入校選考試験問題

問９ 試験問題

次の（１）、（２）の問いに答えなさい。

（１）下図のような直角二等辺三角形ＡＢＣを直線Ｌの上ですべらずに転がしていくと、頂点Ｂの描く軌跡はどのようになるか。次の１から５のうち番号で答えなさい。

三角形を転がした時の頂点の軌道

（２）下図の三角形ＡＢＣにおいて、辺ＢＣを延長したとき∠Ｘの大きさを求めなさい。

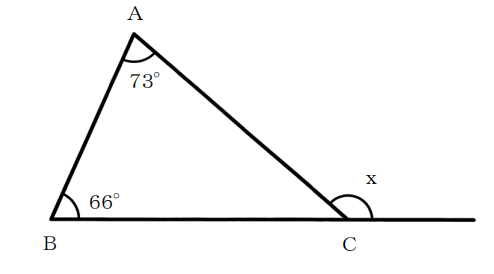
三角形の外角

※以下は解答と解説ですが、見る前にまずは、自分自身でしっかりと解いてみてください。

解答と解説

解答と解説を記載していきます。
解き方が分からないという人を少しでも減らすためにできる限り分かり易く必要以上に細かく順を追って解説している部分がありますが、実際の試験時は丁寧に計算し過ぎると時間のロスに繋がるため、自分の分かるところは効率よく解答していくようにしてください。

■目次

  1. 問題（１）の解答と解説
  2. 問題（２）の解答と解説

問題（１）の解答と解説

試験問題（１）の解答：3

こういった問題は、実際に問題用紙の余白などを使って自分自身で転がした図を描いてみると分かりやすいと思います。下図は、直角二等辺三角形を転がした際の図形です。

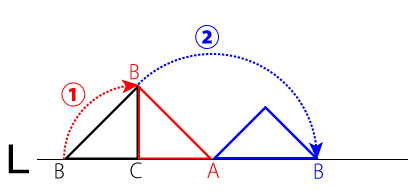
三角形を転がした時の頂点の軌道

①と②の軌道を分けて説明していきます。

①の軌道のときは、辺ＢＣが半径で頂点Ｃが中心とした円軌道でＢ点は移動します。

次に②の軌道は、辺ＡＢが半径で頂点Ａが中心となる円軌道でＢは移動します。辺ＢＣより辺ＡＢの方が長いので、②はより大きな円軌道になります。

この時点で解答を見ると該当するのは3番しかありません。よって、頂点Ｂが描く軌道は3番

問題（２）の解答と解説

試験問題（２）の解答：139°

三角形の内角の和は180°なので、∠ACBは次のようになります。

∠ACB＝180－73－66＝41°

よって、∠Ｘは次の通り。

∠Ｘ＝180－41＝139°

別解
上記は丁寧に解きましたが、三角形の外角は以下が成り立ちます。

『三角形の外角は、その外角に隣り合う内角以外の他の２つの内角の和に等しい』

要は、今回の問題であれば以下の式が成り立ちます。

∠Ｘ＝∠Ａ＋∠Ｂ
　　＝73°＋66°
　　＝139°

※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。