この問題は平成28年4月入校の東京都立職業能力開発センター入校選考試験問題の問2の(1)と(2)の解答と解説です。
問1および、問2の(3)~(5)に関しては以下のページに解説をまとめているので参考にして下さい。
実際の試験の問題用紙は以下のページで確認することができます。
■目次
試験問題 問2(1)
ある美術館の入場料は、35人以上の団体になると20%引きになります。この美術館に30人のグループが入場したときよりも、35人のグループが入場したほうが3000円安くなります。団体割引のない1人あたりの入場料は何円ですか。ただし、消費税は考えないものとします。
解答と解説
問2(1)の解答:1500円
団体割引のない1人あたりの入場料をN円と仮定します。
30人グループが入場した時の入場料合計は次の通り。
入場料=30N・・・①
35人グループが入場する場合は、20%引きとなるので通常の入場料の80%(8割)の価格ということになります。よって、35人グループが入場した時の入場料合計は次の通り。
入場料=35×(N×0.8)
=28N・・・②
30人のグループが入場したときよりも、35人のグループが入場したほうが3000円安くなるということより以下の式が成り立ちます。
①=②+3000
30N=28N+3000
2N=3000
N=1500
よって、団体割引のない1人あたりの入場料は1500円
試験問題 問2(2)
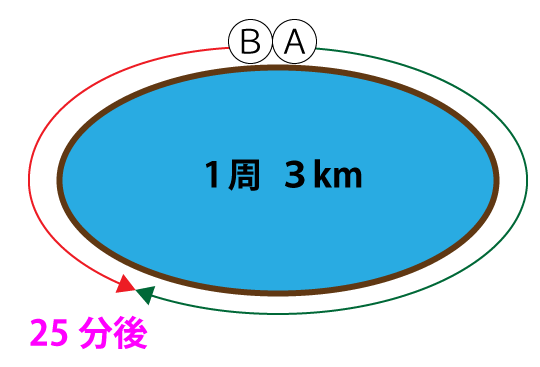
1周3kmの池があります。この池の周囲をAさんとBさんが、ある地点から同時に反対方向に進むと25分後に出会います。同じ方向に進むと、2時間30分後にAさんがBさんに追いつきます。このとき、Aさんの進む速度は分速何mですか。
解答と解説
問2(2)の解答:分速70m
この問題を解くには速度と距離と時間を求める公式を知っている必要があります。

Aさんの進む速度を分速Nメートル、Bさんの進む速度を分速Mメートルと仮定します。
ある地点から同時に反対方向に進むと25分後に出会うということなので、AさんとBさんの25分間の移動距離の合計が池の1周の距離3kmになります。
Aさんの移動距離=速度×時間
=N×25
=25N メートル・・・①
Bさんの移動距離=速度×時間
=M×25
=25M メートル・・・②
AさんとBさんの移動距離合計(①+②)が3kmとなるので以下の式が成り立ちます。
25N+25M=3000
N+M=120・・・③
注意点としては、速度の単位が『分/m』なので3kmをmに統一して計算する必要があります。
次に同じ方向に進むと、2時間30分後にAさんがBさんに追いつくという点からAさんがBさんを1周分(3km)の周回遅れにすることになります。
AさんとBさんは速度差の分だけ徐々に距離が開いていきます。よって、その速度差の速度で2時間30分かけて3kmの差が生じることをになるので以下の式が成り立ちます。
距離=速度×時間
3000=(N-M)×150
N-M=20・・・④
この時も距離(3km=3000m)と時間(2時間30分=150分)の単位を統一して計算するのを忘れないようにしてください。速度の単位が『分/m』なので分とメートルに統一します。
③式+④式をすると求めたいAさんの進む速度Nが求まります。
N+M=120・・・③
N-M=20・・・④
(N+M)+(N-M)=120+20
2N=140
N=70
Aさんの進む速度は、分速70m
※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。

