東京 職業訓練 試験問題[筆記試験] 数学-問2(3)(4)【平成28年4月生】

試験問題 問２(３)

２つのサイコロＡ、Ｂがあります。サイコロＡの出る目をａ、サイコロＢの出る目をｂとするとき、（２ａ＋ｂ）の値が３の倍数となる確率はいくつですか。分数で求めなさい。

解答と解説

問２(３)の解答：1/3

確率を求めるには、『あり得る組み合わせ総数』と『事象が起きる組み合わせ数』が必要になるため組み合わせ数を求める公式を知っている必要があります。

この問題を解く流れは次の通りです。

あり得る組み合わせ総数を求める

サイコロ２つを振って出る目の組み合わせ総数がこれに該当します。サイコロＡＢともに１～６の６つの目があるので、出る目の組み合わせ総数は次の通り。

出る目の組み合わせ総数＝6×6
　　　　　　　　　　　＝36通り。

事象が起きる組み合わせ数を求める

『事象が起きる組み合わせ数』とは、この場合、（２ａ＋ｂ）の値が３の倍数となる組み合わせ数になります。

（２ａ＋ｂ）が最小となるのはａとｂが共に１のときで３となります。逆に最大になるのはａとｂが共に６のときで１８となります。よって、３～１８の数字の中で３の倍数を抜き出します。そうすると『3,6,9,12,15,18』次の６つの値が該当してきます。

よって、以下の６つの式が成り立つａとｂの組み合わせ数を求めればよいことになります。

• 2ａ+ｂ＝3のとき(a,b)=(1,1)
• 2ａ+ｂ＝6のとき(a,b)=(1,4),(2,2)
• 2ａ+ｂ＝9のとき(a,b)=(2,5),(3,3),(4,1)
• 2ａ+ｂ＝12のとき(a,b)=(3,6),(4,4),(5,2)
• 2ａ+ｂ＝15のとき(a,b)=(5,5),(6,3)
• 2ａ+ｂ=＝8のとき(a,b)=(6,6)

よって、（２ａ＋ｂ）の値が３の倍数となる組み合わせ数は12通りとなります。

確率を求める

出る目の組み合わせ総数が36通り、（２ａ＋ｂ）の値が３の倍数となる組み合わせ数は12通りなので（２ａ＋ｂ）の値が３の倍数となる確率は次の通り。

確率＝12/36＝1/3

試験問題 問２(４)

１辺が10cmの正方形があります。この正方形の横の長さをＸ％伸ばし、縦の長さを（Ｘ＋３）％縮めて長方形にしたとき、もとの正方形の面積より3.1％小さくなりました。このとき、Ｘの値はいくつですか。

解答と解説

問２(４)の解答：2
元の正方形は1辺が10cmなので、面積は次の通りとなります。

正方形の面積＝10×10
　　　　　　＝100cm²・・・①

次に変形後の長方形の面積について考えていきます。ここの計算は間違いやすいのでまずは図式化しておきます。

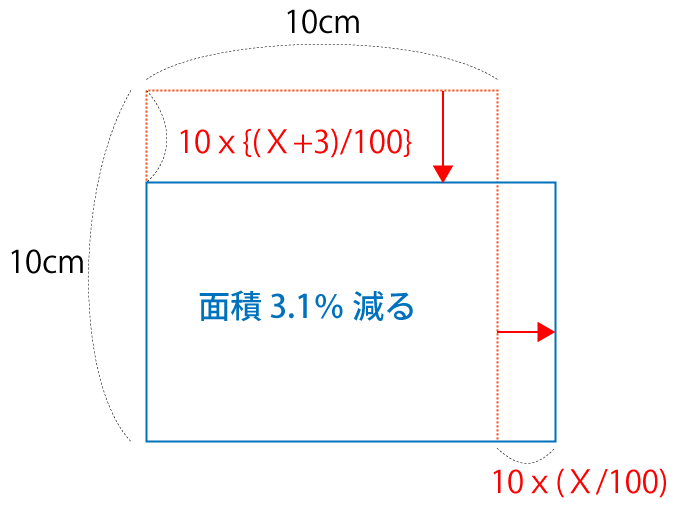
まず、横の長さがＸ％伸びるということなので、伸びた長さは次の通り。

横の伸びた長さ＝10×(Ｘ/100)
　　　　　　　＝Ｘ/10

縦の長さは(Ｘ＋3)％縮めるとのことなので、縮んだ長さは次の通り。

縦の縮んだ長さ＝10×{(Ｘ＋3)/100}
　　　　　　　＝(Ｘ＋3)/10

※Ｘは％なのでそのままＸをかけるのではなく100で割ることを忘れないようにしてください。

よって、長方形の横の長さは「10＋Ｘ/10」、縦の長さは「10－(Ｘ＋3)/10」となります。そして、変形後の面積は次の通り。

変形後の面積＝(10＋Ｘ/10)×{10－(Ｘ＋3)/10}
　　　　　　＝100－(Ｘ＋3)＋Ｘ－Ｘ(Ｘ＋3)/100
　　　　　　＝97－Ｘ(Ｘ＋3)/100・・・②

元の正方形から面積が3.1％減るということは、変形後の長方形の面積は元の正方形の面積の96.9％だとわかります。よって、その面積は次の通り。

変形後の面積＝正方形の面積×(96.9/100)
　　　　　　＝100×(96.9/100)
　　　　　　＝96.9

よって、この面積が②の面積を等しくなるはずなので以下の式が成り立ちます。

97－Ｘ(Ｘ＋3)/100＝96.9
9700－Ｘ²－3Ｘ＝9690
Ｘ²＋3Ｘ－10＝0
(Ｘ＋5)(Ｘ－2)＝0
Ｘ＝－5と2

本来であれば解答は－5と2の両方なのですが、実際の解答を確認すると2だけになっています。

－5の場合、問題文に当てはめると「正方形の横の長さを－5％伸ばし・・・」、「縦の長さを－2％縮めて・・・」と不自然な表現になってしまうため問題作成者としては「2」だけを解答として考えているのだと思いますが、解答としては－5もあり得るのでやや不親切な問題だと言えます。

※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。