この問題は平成30年7月入校の東京都立職業能力開発センター入校選考試験問題の問2の(1)と(2)の解答と解説です。
問1および、問2の(3)~(5)に関しては以下のページに解説をまとめているので参考にして下さい。
実際の試験の問題用紙は以下のページで確認することができます。
■目次
試験問題 問2(1)
濃度9%の食塩水50gに、水を加えて濃度3%の食塩水を作ります。このとき、加える水の量は何gですか。
解答と解説
問2(1)の解答:100g
この問題を解くには食塩水の濃度を求める公式を知っている必要があります。

加える水の量をXgとし、問題文より分かっていることを図式化すると下図のようになります。

まずは、容器Aに入っている食塩の量(重さ)を公式より算出します。
食塩水の濃度=食塩の重さ÷食塩水の重さ×100
食塩の重さ=食塩水の濃度×食塩水の重さ÷100
=0.09×50
=4.5g
容器Aに入っている食塩は4.5gと分かりました。容器Bは単なる水なので容器AとBを合わせたとき容器Cに含まれる食塩の量も4.5gになります。
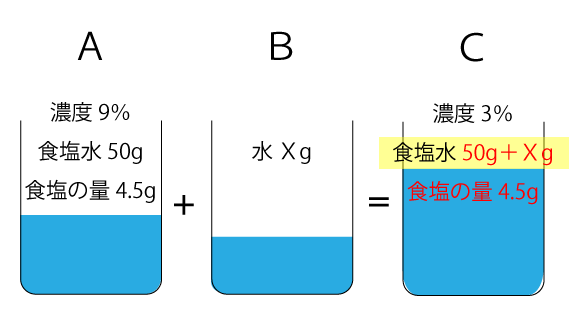
容器Cの濃度と食塩の量が分かったので容器Cの食塩水の量を求めます。
食塩水の重さ=食塩の重さ÷食塩水の濃度×100
50+X=4.5÷3×100
50+X==1.5×100
50+X==150
X=100
よって、加える水の量は100g
試験問題 問2(2)
2けたの自然数があります。その自然数は、十の位の数と一の位の数の和の9倍より9小さくなります。また十の位の数と一の位の数を入れかえてできる数は、もとの自然数より45小さくなります。もとの自然数を求めなさい。
解答と解説
問2(2)の解答:72
自然数の十の位の数字をa、一の位の数字をbと仮定すると元の自然数は以下のようにあらわすことができます。
元の自然数=a×10+b
さらに元の自然数は、十の位の数と一の位の数の和の9倍より9小さくなるということなので、次のようになります。
a×10+b=(a+b)×9-9
10a+b=9a+9b-9
a-8b+9=0・・・①
また十の位の数と一の位の数を入れかえてできる数は、もとの自然数より45小さくなるということなので以下の式が成り立ちます。
b×10+a=(a×10+b)-45
10b+a=10a+b-45
9a-9b-45=0
a-b-5=0・・・②
式①-式②をしてaとbの値を求めていきます。
a-8b+9=0・・・①
a-b-5=0・・・②
————-
(a-8b+9)-(a-b-5)=0
-7b+14=0
b=2
bの値が求まったので、式①もしくは式②に代入しaの値も求めます。
a-b-5=0・・・②
a-2-5=0
a=7
よって、もとの自然数は72
※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。

