この問題は平成30年7月入校の東京都立職業能力開発センター入校選考試験問題の問2の(3)と(4)の解答と解説です。
問1および、問2の(1)(2)(5)に関しては以下のページに解説をまとめているので参考にして下さい。
実際の試験の問題用紙は以下のページで確認することができます。
■目次
試験問題 問2(3)
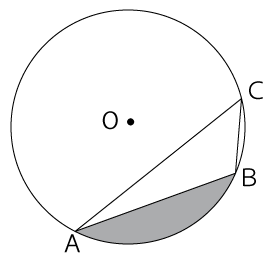
図のような円Oの円周上に3点A、B、Cをとります。AB=4cm、∠CAB=20°、∠ABC=115°のとき、塗りつぶした部分の面積は何cm²ですか。
解答と解説
問2(3)の解答:2π-4 cm
この問題を解くには円周角の定理と三平方の定理を知っている必要があります。
まずは、問題文から分かっている点を図に書き込むと下図のようになります。
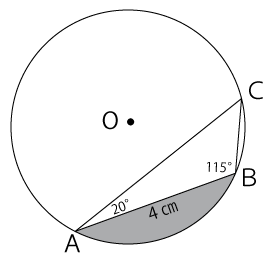
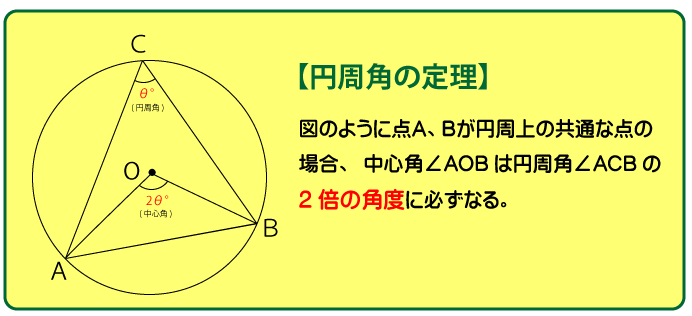
∠CAB=20°、∠ABC=115°と分かっているので、∠ACB=45°だとわかります。また、円の中心Oと円周上の点ABを結んだ△AOBを作ると、円周角の定理より∠AOB=90°だとわかります。
∠AOB=∠ACB×2
=45°×2
=90°
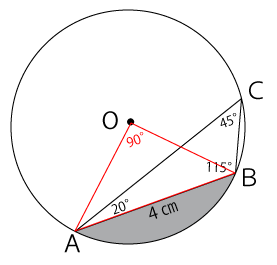
OAとOBは円の半径なので、△AOBは直角二等辺三角形だと分かります。よって、三平方の定理が利用できるので三平方の定理を利用して円の半径であるOA、OBの長さを求めます。
OA=OB=Rと仮定します。
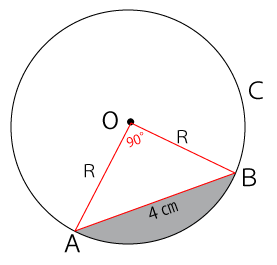
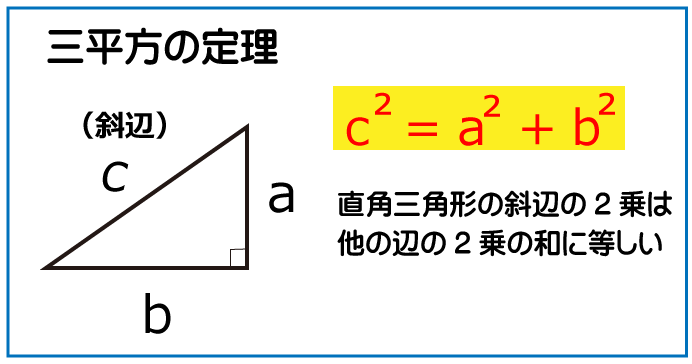
三平方の定理
AB²=OA²+OB²
16=R²+R²
2R²=16
R²=8
R=2√2
円の半径Rは、2√2だと分かりました。
求めたい部分の面積(灰色部分)は、円の面積から扇形の面積(黄色部分)と直角二等辺三角形の面積(赤色部分)を引いた面積になります。
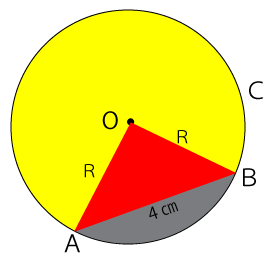
求めたい面積=円の面積-扇形の面積-三角形の面積
円の面積
円の半径は2√2だと分かったので、面積は次の通り。
円の面積=半径×半径×π
=2√2×2√2×π
=8π・・・①
扇形の面積
△AOBは直角三角形なので扇形の中心角は360-90=270°だとわかります。よって、これは真円の3/4の大きさなので扇型の面積は真円の3/4の大きさになります。
扇形の面積=①×3/4
=8π×3/4
=6π・・・②
三角形の面積
三角形の底面をOAとした場合、高さはOBとなりいずれも半径の長さにあたります。よって、△AOBの面積は次の通り。
△AOBの面積=2√2×2√2÷2
=4・・・③
求めたい部分の面積
求めたい面積=円の面積①-扇形の面積②-三角形の面積③
=8π-6π-4
=2π-4
よって、求めたい部分の面積は、2π-4 cm
試験問題 問2(4)
図のように0、1、2、3、4の数字を1つずつ記入した5枚のカードがあります。このカードから2枚を同時に取り出すとき、カードの数字の和が5である確率を分数で求めなさい。

解答と解説
問2(4)の解答:1/5
この問題を解くには組み合わせの公式を知っている必要があります。

求めたい確率は以下の式で求まります。
求めたい確率=(カードの数字の和が5になる組み合わせ数)÷(5枚のカードから2枚を抜き出す組み合わせ数)
カードの数字の和が5になる組み合わせ数
カードの数字の和が5になる組み合わせ数は、『1と4』、『2と3』の2通りしかありません。
5枚のカードから2枚を抜き出す組み合わせ数
5枚のカードから2枚を抜き出す組み合わせ数は、組み合わせの公式より次の通りになります。
₅C₂=(5×4×3×2×1)/{(2×1)(3×2×1)}
=(5×4)/(2×1)
=20/2
=10通り
求めたい確率
求めたい確率=(カードの数字の和が5になる組み合わせ数)÷(5枚のカードから2枚を抜き出す組み合わせ数)
=2/10
=1/5
よって、求めたい確率は1/5
※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。

