この問題は平成30年7月入校の東京都立職業能力開発センター入校選考試験問題の問２の（５）の解答と解説です。

問１および、問２の（１）～（４）に関しては以下のページに解説をまとめているので参考にして下さい。

実際の試験の問題用紙は以下のページで確認することができます。

⇒都立職業能力開発センター入校選考試験問題(平成30年7月生)

試験問題 問２(５)

図の直角三角形ＡＢＣは、辺ＢＣ＝８cm、∠Ｃ＝30°、∠Ａ＝90°です。このとき、辺ＢＣを軸として１回転させてできる立体の体積は何cm³ですか。

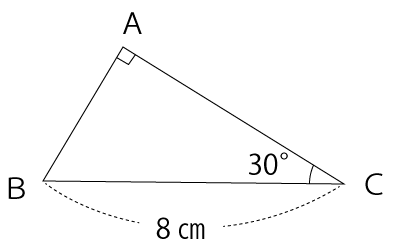
直角三角形

解答と解説

問２(５)の解答：32㎝³

この問題を解くには、円すいの体積を求める公式を知っている必要があります。

円すいの体積を求める公式

△ABCを辺BCを軸に1回転させると下図のようになります。

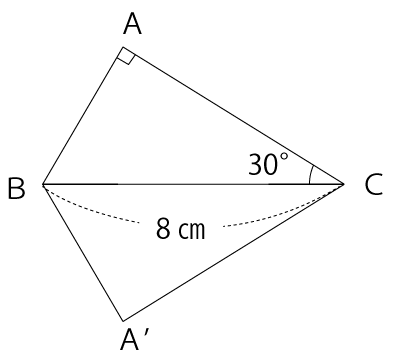
三角形を回転

この立体の体積を求める場合、立体を点Ａと点Ａ’を結んだ線で2つに分割し、2つの円すいに分けて体積を求めていきます。

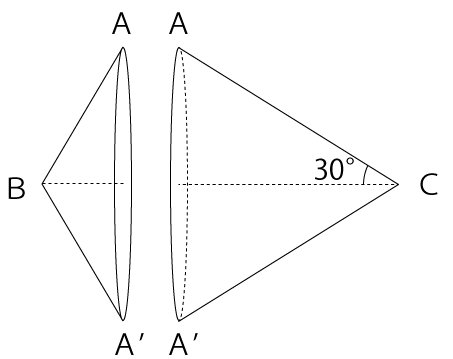
二つの円すい

体積を求める前にまずは、分かる辺の長さや角度を図に書き込んでいきます。
∠ACB＝30°、∠A＝90°なので∠ABC＝60°となります。よって、以下の特別な直角三角形の3辺の比が適用できます。

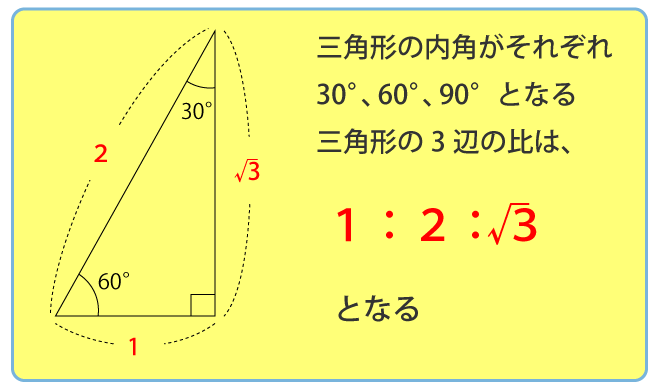
特別な三角形の比

特別な直角三角形の3辺の比より、辺BCが8㎝なので以下の比が成り立ちます。
1：2：√3＝AB：BC：AC
1：2：√3＝AB：8：AC
1：2：√3＝4：8：4√3

AB＝4
BC＝8
AC＝4√3

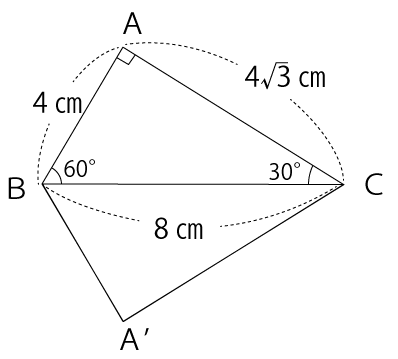
特別な三角形の各辺の長さ

次に2つの円すいに分けたときに円すいの底面となる円の半径を求めていきます。

点Ａから辺BCに垂線を下ろし、交わる点をＯとします。そうすると、内角が30°、60°、90°の特別な直角三角形ＡＢＯができます。

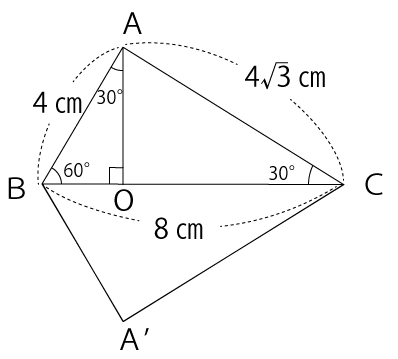
特別な直角三角形を作る

ここで再度、特別な直角三角形の3辺の比を利用しＡＯ、ＢＯ、ＯＣの長さを求めていきます。

1：2：√3＝BO：AB：AO
1：2：√3＝BO：4：AO
1：2：√3＝2：4：2√3

BO＝2
AB＝4
AO＝2√3

OC＝8－2＝6

図に書き込むと下図のようになります。

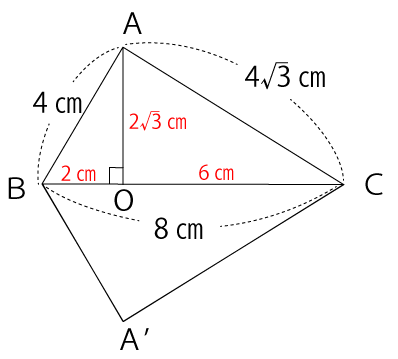
特別な直角三角形の各辺の長さ

円すいの体積を求めるのに必要な情報がそろったので、円すいABA’と円すいACA’の2つに分けて、それぞれの体積を求めていきます。

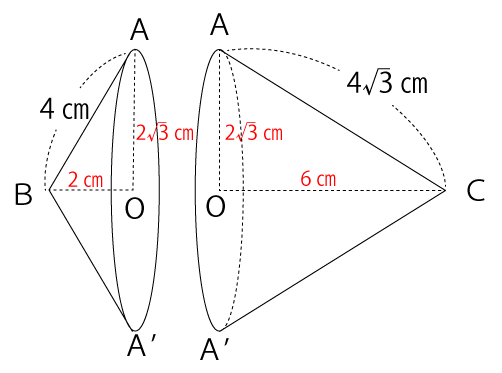
二つの円すいの体積

円すいABA’の体積＝底面積×高さ÷3
　　　　　　　　＝(2√3×2√3×π)×2÷3
　　　　　　　　＝12π×2÷3
　　　　　　　　＝8π

円すいACA’の体積＝底面積×高さ÷3
　　　　　　　　＝(2√3×2√3×π)×6÷3
　　　　　　　　＝12π×6÷3
　　　　　　　　＝24π

よって、求めたい辺ＢＣを軸として１回転させてできる立体の体積は8π＋24π＝32π㎝³

※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。