大阪 職業訓練 試験問題 数学-問4(平成28年8月26日実施) 普通課程

図は1辺の長さが4の立方体である。以下の問いに答え なさい。

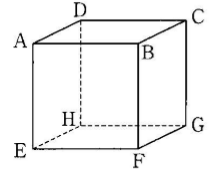
[問題1]　△BDEの面積を求めなさい。

[問題2]　点Aから平面BDEに下ろした垂線と平面BDEとの交点をPとする。APの長さを求めなさい。

解答と解説

試験問題１の解答：イ
三角形BDEの一辺の長さは三平方の定理を使って求めます。

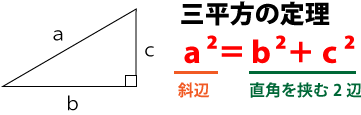
三角形ABDに着目して、BDの長さを求めてみます。
「AD＝AB＝4」なので、三平方の定理BDは次の通りになります。

BD²＝4²＋4²
BD²＝16＋16
BD²＝32
BD＝√32
BD＝4√2

「BD＝ED＝BE」なので三角形BDEは一辺が4√2の正三角形になります。

ここで、正三角形の面積を求める公式を知っていれば簡単に解答を求めることができるのですが、頭に入れていない人も多いと思うので、公式を使わない場合の解き方も記載しておきます。

公式を使用する解き方
正三角形の面積を求める公式は次の通り。

面積＝(√3/4)ａ²

これを使用すると正三角形の面積は次の通り。

面積＝(√3/4)ａ²
　　＝(√3/4)x(4√2)²
　　＝(√3/4)x32
　　＝8√3

試験問題２の解答：オ
APは、三角形BDEを底面、頂点をAとした三角錐BDE-Aの高さになります。

APの求め方の流れとしては、まずは三角錐BDE-Aの体積を求めた後、その体積から高さAPを求めます。とはいえ、高さが分からないのにどうやって三角錐の体積を求めるか？三角錐BDE-Aは、三角形ABDを底面、頂点をEとした三角錐ABD-Eでもあります。三角錐ABD-Eの高さAEは4、あとは底面積となる三角形ABDの面積が分かれば三角錐の体積を求めることができます。

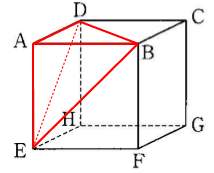
三角形ABD三角形ABDの面積は次の通り。

△ABDの面積＝4×4÷2＝8

三角錐ABD-Eの体積

三角錐の体積を求める公式
体積＝底面積x高さ÷3

よって、三角錐ABD-Eの体積は次の通り。
体積＝8×4÷3
　　＝32/3 ㎝³

三角錐ABD-Eは、三角錐BDE-Aでもあるので、体積はどちらも32/3 ㎝³になります。この問題で問われているのは三角錐BDE-Aの高さに相当するABの長さ。問題1の三角形BDEの面積と体積の公式から次の式が成り立ちます。

三角錐の体積＝底面積x高さ÷3
32/3＝8√3x(高さAP)÷3
高さAP＝32/8√3
　　　＝4/√3
　　　＝4√3/3

※解説を記載するまでもないと判断した問題に関しては、解説を記載せず解答のみを記載しています。もし、この問題の解説が欲しいというのがあれば、コメント欄に記載してください。また、記載している解説の内容も不明であれば遠慮なくコメントください。