問1~2、問4に関しては以下のページに解説をまとめているので参考にして下さい。
大阪 職業訓練 短期過程試験問題 数学-問1
大阪 職業訓練 短期過程試験問題 数学-問2
大阪 職業訓練 短期過程試験問題 数学-問4
図は∠A=120°で、AB=4cm、BC=5cmの平行四辺形である。以下の問いにア~オから選んで答えなさい。
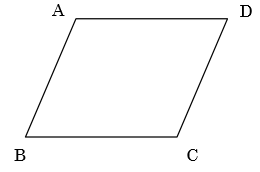
[問題1] ∠ABCの大きさを求めなさい。
[解答群]
ア 30° イ 45° ウ 60° エ 75° オ 80°
[問題2] 点Aと点Cを結んで対角線ACを引く。このときACの長さを求めなさい。
[解答群]
ア 3 cm イ √15 cm ウ 3√2 エ √21 オ 3√5
解答と解説
試験問題1の解答:ウ
四角形ABCDは平行四辺形なので、「∠A+∠B=180°」が成り立ちます。よって、∠B=∠ABCは次の通り。
∠B=∠ABC=180-120=60°
試験問題2の解答:エ
——————————-
※補足
この問題を解くには以下の2点を知っておく必要がある。
- 三平方の定理
- 直角三角形の各辺の比率
1.三平方の定理
三角形が直角三角形の場合、斜辺の長さをa、その他の2辺をb、cとすると次の式が成り立ちます。
a²=b²+c²
2.直角三角形の各辺の比率
直角三角形の3つの内角が、90°、60°、30°の場合、各辺の比率は次のようになる。
1:2:√3
——————————–
頂点Aから辺BCに垂線を下し、辺BCとの交点をEとした場合、直角三角形ABEができあがります。また、∠Aが120°ということから∠Bは60°(180°-120°)だと分かります。
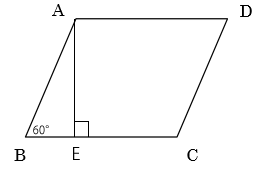
このことより、この直角三角形は内角が90°、60°、30°となる三角形で各辺の比率が「1:2:√3」となります。辺ABは直角三角形ABEの斜辺で長さは4㎝と分かっているので各辺の比率より次のことが言えます。
BE:AB:AE=1:2:√3
AB=4㎝なので各辺の長さは次の通り。
AB=4
BE=AB/2=2
AE=(√3/2)xAB=2√3
次に三角形AECについて見ていきます。三角形AECも辺ACを斜辺とした直角三角形になります。直角三角形AECの各辺の長さは次の通り。
辺AE=2√3
辺EC=5-2=3
辺ACは三平方の定理を使用して求めます。
a²=b²+c²
AC²=AE²+EC²
AC²=(2√3)²+3²
AC²=12+9
AC²=21
AC=√21 ㎝
※解説を記載するまでもないと判断した問題に関しては、解説を記載せず解答のみを記載しています。もし、この問題の解説が欲しいというのがあれば、コメント欄に記載してください。また、記載している解説の内容も不明であれば遠慮なくコメントください。

