問1~2、問4に関しては以下のページに解説をまとめているので参考にして下さい。
大阪 職業訓練 短期過程試験問題 数学-問1
大阪 職業訓練 短期過程試験問題 数学-問2
大阪 職業訓練 短期過程試験問題 数学-問4
図のように1辺の長さが8cmの立方体がある。ABの中点をM、BCの中点をNとするとき、以下の問いにア~オから選んで答えなさい。
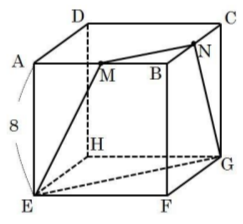
[問題1] EM、FB、GNの延長の交点をPとするとき、PBの長さを求めなさい。
[解答群]
ア 4cm イ 6cm ウ 8cm エ 10cm オ 16cm
[問題2] 三角すい台MBN-EFGの体積を求めなさい。
[解答群]
ア 448/3 cm³ イ 412/3 cm³ ウ 331/3 cm³ エ 150 cm³ オ 418/3 cm³
[問題3] 台形MNGEの面積を求めなさい。
[解答群]
ア 144 cm² イ 24√19 cm² ウ 56 cm² エ 72 cm² オ 36√2 cm²
解答と解説
試験問題1の解答:ウ
下図の様に同じ正立方体を上にのせて考えると分かりやすい。
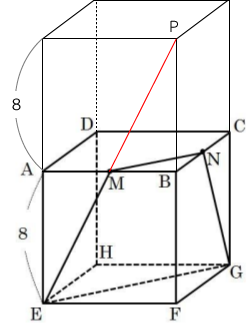
四角形ABEFは正四角形で、ABの中点である点Mを通りEMを延長していくと、点Pは上図の通りFP=2FBの点で交わる。よって、PB=8となる。
試験問題2の解答:ア
三角すい台MBN-EFGの体積は、三角錐P-EFGの体積から三角錐P-MBNの体積を引けば求まる。
三角台錐MBN-EFG体積=(三角錐P-EFG体積)-(三角錐P-MBN体積)
三角錐の体積を求める公式は次の通り。
三角錐の体積=底面積x高さ÷3
三角錐P-EFGの体積
底面となる三角形EFGの面積
8x8÷2=32
高さとなるPFの長さは16。よって、三角錐P-EFGの体積は次の通り。
三角錐の体積=底面積x高さ÷3
=32x16÷3
=512/3
三角錐P-MBNの体積
底面となる三角形MBNの面積
4x4÷2=8
高さとなるPBの長さは8。よって、三角錐P-MBNの体積は次の通り。
三角錐の体積=底面積x高さ÷3
=8x8÷3
=64/3
三角台錐MBN-EFGの体積
512/3-64/3=448/3 cm³
試験問題3の解答:エ
この問題の解き方は、「三平方の定理を駆使して解く方法」と「三角錐の図形を展開し解く方法」の二通りがあります。ここでは三平方の定理を利用して解きます。
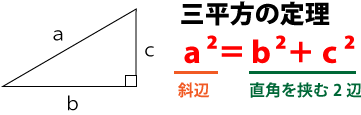
大まかな解く流れは次の通り。
- 三角形PEGの面積を求める。
- 三角形PMNの面積を求める。
- 台形MNGEの面積を求める。
三角形PEGの面積を求める
EGの長さは三平方の定理より次の通り。
EG²=EF²+FG²
EG²=8²+8²
EG²=128
EG=√128
EG=8√2
PEの長さは三平方の定理より次の通り。
PE²=EF²+PF²
PE²=8²+16²
PE²=320
PE=8√5
点PからEGに対して垂線を下ろし、その交点をOとした場合、POの長さは三平方の定理より次の通り。
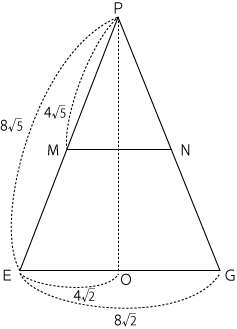
PE²=PO²+EO²
(8√5)²=PO²+(4√2)²
320=PO²+32
PO²=288
PO=√288
PO=12√2
三角形PEG面積=EGxPO÷2
三角形PEG面積=8√2x12√2÷2
三角形PEG面積=96
三角形PMNの面積を求める
点PからMNに垂線を下ろし、その交点をQとする。三角形PMNは三角形PEGの1/2の大きさなので各辺の長さも全て1/2となるはずだが、念のため下記に計算してみます。
MNの長さは三平方の定理より次の通り。
MN²=MB²+BN²
MN²=4²+4²
MN²=32
MN=4√2
PQの長さは三平方の定理より次の通り。
PM²=MQ²+PQ²
(4√5)²=(2√2)²+PQ²
80=8+PQ²
PQ²=72
PQ=6√2
三角形PMNの面積=MNxPQ÷2
三角形PMNの面積=4√2x6√2÷2
三角形PMNの面積=24
台形MNGEの面積を求める
台形MNGEの面積=96-24=72cm²
※解説を記載するまでもないと判断した問題に関しては、解説を記載せず解答のみを記載しています。もし、この問題の解説が欲しいというのがあれば、コメント欄に記載してください。また、記載している解説の内容も不明であれば遠慮なくコメントください。

