平成27年度に埼玉県で実施された職業訓練(短期コース)の選考試験で出題された試験問題と、その解答と解説です。 本ページでは数学問題の問題2(正式なテスト用紙上では設問6)のみ記載しています。その他の問題に関しては、以下のページを参照してください。
埼玉 職業訓練 試験問題[短期] 数学-問1(平成27年入校生)
埼玉 職業訓練 試験問題[短期] 数学-問3(平成27年入校生)
埼玉 職業訓練 試験問題[短期] 数学-問4(平成27年入校生)
試験問題 設問2
6. 次の問いに答えなさい。
[問題1]
縦84メートル、横120メートルの長方形の校庭の周りに、等しい間隔で木を植えたいと思う。植える木はできるだけ少なくし、4すみには必ず植えることとする。木は全部で何本必要になるか。
[問題2]
池の周りを1周する道がある。この道を兄は分速90メートル、弟は分速60メートルで歩く。2人が同じ場所から反対の方向に同時に歩き始めたら、出発してから
10分後に出会った。この道の1周の道のりは何メートルか。
解答と解説
試験問題1の解答:
現実的に考えると気の太さも考慮する必要がありますが、この問題では気の太さについては触れられていないので無視して構わない。重要なポイントとしては次の2点。
- 四隅に必ず木は植えられる
- 等しい間隔で木は植えられる
例えば、84m間隔で木を植えようとした場合、横が等間隔にならない。
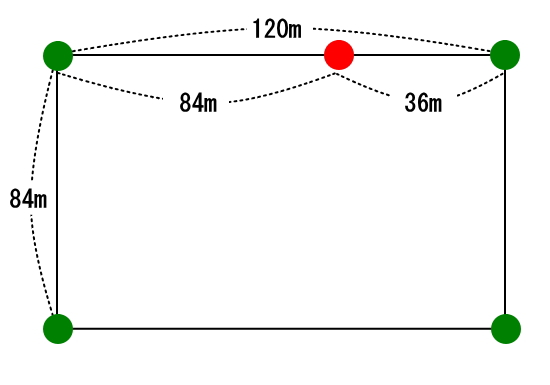
横と縦に等間隔でかつ、植える本数を最も少なくしたい場合は、84と120の約数で最大の数値、いわゆる最大公約数を求めればいい。最大公約数の求め方は最近では色々でてきますが、一般的な計算方法は、下記のように84と120の2つの数値を割れなくなるまで割ったところで赤丸内の数値を掛けたものが最大公約数となります。
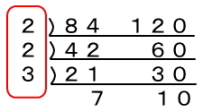
よって、最大公約数は次の通り。
2x2x3=12
このことより12m間隔で木を植えるのが最も少ない本数で植えれることがわかります。では、12m間隔で木を植えた場合、何本の木が植えられるのか?これは、長方形の校庭で考えるより、長方形を下図のように一本の線に広げて考えた方が分かりやすいかもしれません。

ただし、注意点として図のA地点とB地点は本来同じ地点なので、木の数を数える際は1本多くなってしまわないように注意して下さいね。校庭の周囲408m(84+84+120+120)に12m間隔で木を植えた場合、植えられる本数は次の通り。
408÷12=34本
解答:34本
試験問題2の解答:
問題より分かっている点を図に落とし込むと下図のようになります。
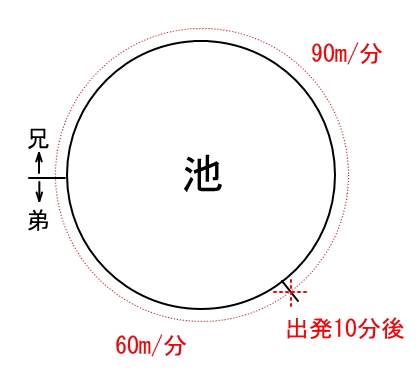
求めるのは池の周囲。これを求めるのには、下記の距離・速度・時間の関係(公式)を覚えておく必要があります。
距離=速度x時間
※補足
覚えるのが苦手と言う人は、下記で覚えておく方が覚えやすいかもしれませんね。
速度=距離/時間
車やバイクのスピードメーターの単位はkm/hですよね。これは「速度=距離(km)/時間(h)」を意味しています。
公式を使って兄と弟の歩いた距離の合計を求めれば、それが池の周囲の距離になります。
兄の歩いた距離
距離=速度x時間
=90x10
=900m
弟の歩いた距離
距離=速度x時間
=60x10
=600m
2人の歩いた距離合計
2人の歩いた距離の合計は、
900m+600m=1500m
よって、池の周りの道1周の距離は、1500m
解答:1500m

