次の問に答えなさい。
[問題1] 現在、兄は13歳、弟は10歳、父は39歳です。兄と弟の年齢の和が父の年齢と等しくなるのは何年後ですか。
[問題2] ある選手が42.195kmの道のりを2時間20分39秒で走りました。このとき、平均速度は時速何kmですか。
[問題3] 濃度がわからない食塩水A、Bを同量混ぜ合わせると濃度15%の食塩水ができ、食塩水A50gと食塩水B150gを混ぜ合わせると濃度17%の食塩水ができます。このとき、食塩水Aの濃度は何%ですか
[問題4] 男子3人と女子4人の中から、男子2人と女子1人を選びます。このとき、組み合わせは全部で何通りありますか。
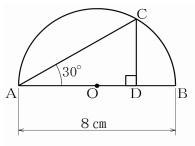
[問題5] 図のように、点Oを中心とし、ABを直径とする半円があります。円弧上の点Cから直径ABに垂線を引き、交点を点Dとします。AB=8㎝、∠CAB=30°のとき、CDの長さは何cmですか。
解答と解説
試験問題1の解答:
求めたい兄と弟の年齢の和が父の年齢と等しくなるのをX年後とします。そうすると、次の式が成り立ちます。
(13+X)+(10+X)=39+X
この式を解くと求めたいXの値が出てきます。
(13+X)+(10+X)=39+X
2X+23=39+X
X=16
解答:16年後
試験問題2の解答:
東京の職業訓練の設問2は毎回、速度に関する問題が出題されます。次の公式は頭にいれておくようにしましょう。
速度=距離÷時間
毎回同じことを書いていますが、上の公式を覚えられない人は次のような覚え方をすれば頭にはいりやすい。
バイクや車などにあるスピードメーターのを思い浮かべてください。『km/h』と表示されていると思います。これは、速度の単位で、
速度=km/h=距離/時間
のことを意味します。簡単ですね。
この問題のポイントは、単位。求められているのは時速何kmか? なので、単位は『時間』と『キロメートル』に統一して計算する必要があります。距離は、42.195㎞と『キロメートル』表示されているので問題ありませんが、時間が『2時間20分39秒』と分、秒が使われています。これを『時間』に変換しなければなりません。
時間の変換
2時間 ⇒ 2時間
20分 ⇒ 20÷60=1/3時間
39秒 ⇒ 39÷60÷60=39/3600=13/1200時間
よって、2時間20分39秒は、
2+(1/3)+(13/1200)
=(2400/1200)+(400/1200)+(13/1200)
=2813/1200 時間
さて、時間の変換が終わったので、公式にあてはめ速度を求めていきます。
速度=距離÷時間
=42.195÷(2813/1200)
=42.195×(1200/2813)
=50634/2813
=18 km/h
解答:時速18㎞
試験問題3の解答:
食塩水の濃度を求める公式は次の通りです。
濃度(%)=食塩(g) ÷ 食塩水の量(g)
数学が苦手な人は一見難しい(涙) と思いがちですが難しく考える必要はありません。食塩水の中に何グラムの食塩が入っているか? が濃度です。なので、食塩の量を食塩水の量で割ると濃度が算出できるのです。
これでも難しいという方は、公式を変形させ、下記の形にすれば覚えやすい?
食塩(g)=食塩水の量(g) × 濃度(%)
例えば、食塩水の量が100g、濃度が50%だったとします。これは、100gの食塩水の内、50%が食塩ですよ。ということを意味します。よって、公式は上記の通りで、実際に当てはめると次の計算になります。
食塩(g)=食塩水の量(g) × 濃度(%)
食塩(g)=100 × 0.5 =50g
※50%=0.5
さて、公式を頭に入れた上で本題に入ります。
まず、前提条件として、食塩水Aの濃度をX%、食塩水Bの濃度をY%とします。そして、設問の前半部分『度がわからない食塩水A、Bを同量混ぜ合わせると濃度15%の食塩水ができる』と、後半部分『食塩水A50gと食塩水B150gを混ぜ合わせると濃度17%の食塩水ができる』を別々にみていきます。
◎前半部分
『濃度がわからない食塩水A、Bを同量混ぜ合わせた』とあるので、このときの食塩水A、Bの量はそれぞれNグラムと仮定します。
食塩Aについて考える
食塩水Aの濃度は、X%
食塩水Aの量は、Nグラム
よって、この時の食塩の量は公式より、
食塩(g)=食塩水の量(g) × 濃度(%)
=N×X
=NX
食塩Bについて考える
食塩水Bの濃度は、Y%
食塩水Bの量は、Nグラム(食塩水Aと同量)
よって、この時の食塩の量は公式より、
食塩(g)=食塩水の量(g) × 濃度(%)
=N×Y
=NY
食塩ABの混合食塩水について考える
混合食塩水の食塩水の量は、N+N なので、2Nグラムとなります。
更に食塩の量は、食塩AがNXグラム、食塩BがYXグラムなので、NX+NYグラムとなります。
そして、濃度は設問より15%になるということなので公式にあてはめると次のようになります。
食塩(g)=食塩水の量(g) × 濃度(%)
NX+NY=2N × 0.15
NX+NY=0.3N
X+Y=0.3 ・・・(1)
◎後半部分
食塩Aについて考える
食塩水Aの濃度は、X%なので、食塩水が50グラムのときの食塩の量は公式にあてはめると次のようになります。
食塩(g)=食塩水の量(g) × 濃度(%)
=50 × X
=50X
食塩Bについて考える
食塩水Bの濃度は、Y%なので、食塩水が150グラムのときの食塩の量は公式にあてはめると次のようになります。
食塩(g)=食塩水の量(g) × 濃度(%)
=150 × Y
=150Y
食塩ABの混合食塩水について考える
食塩水の量は、食塩水Aが50g、食塩水Bが150gなので混合食塩水の量は200g。
食塩の量は、食塩水Aが50X、食塩水Bが150Yなので混合食塩水の食塩の量は、50X+150Y。
そして、この混合食塩水の濃度は設問より17%と分かっているので公式にあてはめると次のようになります。
食塩(g)=食塩水の量(g) × 濃度(%)
50X+150Y=200 × 0.17
50X+150Y=34 ・・・(2)
◎食塩水Aの濃度を求める
式(1)と式(2)の連立方程式を解けば、求めたい食塩水Aの濃度Xを求めることができます。
X+Y=0.3 ・・・(1)
50X+150Y=34 ・・・(2)
求めたいのは、XのほうなのでYを消すように式(1)を式(2)へ代入します。
50X+150Y=34
50X+150(0.3-X)=34
50X+45-150X=34
-100X=-11
X=11/100=11%
解答:11%
試験問題4の解答:
組合せの公式を使います。力技で解けなくもありませんが、ここは公式を使うのが無難です。

男子3人の中から、2人を選ぶ組合せ数は次の通り。
3C2=(3×2)/(2×1)=6/2=3通り
女子4人の中から、1人を選ぶ組合せ数は次の通り。
4C1=4/1=4
よって、男子3人と女子4人の中から、男子2人と女子1人を選ぶ組み合わせ数は、次の通り。
3通り × 4通り = 12通り
解答:12通り
試験問題5の解答:
この問題は、三角関数を使って解く方法、三平方の定理を使って解く方法、三角比を使って解く方法など何通りかの解き方があります。
最も早く解く方法が三角関数を使う方法ですが、三角関数は高校1年で習う解き方なので、職業訓練の試験問題や、SPIなどで三角関数を使う解き方は避けたいところ。よって、最も簡単な三角比を使った解き方で記載したいと思います。
しかし、この三角比で解く場合であっても覚えなければならないことがあります。それが下記に記載する、三角形の各辺の比です。
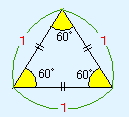
全ての辺の長さは同じで、辺の長さの比は、
辺の長さの比 1:1:1
これは当たり前ですね。
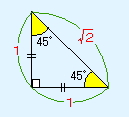
直角を挟む2辺の長さは等しく乗り1辺は√2
辺の長さの比 1:1:√2
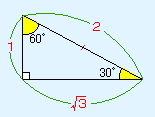
各角が30°、60°、90°となる直角三角形の各辺の長さは次の通り
辺の長さの比 1:2:√3
三角比を頭に入れたら設問に入ります。今回の設問で使用するのは、各角が30°、60°、90°となる直角三角形の三角比のみを使用します。
まずは、下図のように点Cから円の中心に線を引きます。
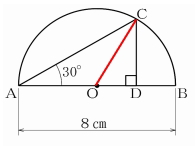
線を引いた線分OCは円の半径なので、次のことが言えます。
線分OA=OC=4cm
よって、三角形AOCは二等辺三角形なので∠OCA=30° と分かります。更に、∠A=30°、∠D=90° なので、∠C=60° だと分かります。よって、∠OCDは、30° (60°-30°)となります。
∠OCDが30° であれば、∠CODは60°となるため、『各角が30°、60°、90°となる直角三角形の三角比』が利用できます。
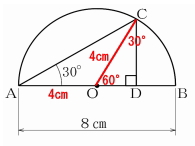
各角が30°、60°、90°となる直角三角形の三角比は、
OD:OC:CD=1:2:√3
辺OCの長さが4cmと分かっているので上記の比は次のようになります。
OD:OC:CD=2:4:2√3
よって、辺CDの長さは、2√3
解答:2√3

