次の問に答えなさい。
[問題1] 鉛筆8本と150円のボールペン1本の代金の合計は、同じ鉛筆2本と60円の消しゴム1個の代金の合計の3倍になります。この鉛筆1本の値段は何円ですか。ただし,消費税は考えないものとします。
[問題2] ある坂道を毎時3kmの速さで登るのと、毎時6kmで下るのでは、所要時間に5分の差が生じます。この坂道の長さは何mですか。
[問題3] 図はある月のカレンダーです。図のように日にちを囲むと、囲まれた数字の和が60になっています。このカレンダーで同じように囲んだときの数字の和が105になるのは,中央の日にちが何日のときですか。

[問題4] 2つの1次関数,Y=aX-1と Y=-X+5(aは定数)のグラフの交点のX座標は2でした。このとき、aの値はいくつですか。
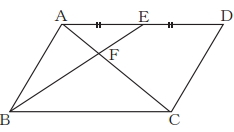
[問題5] 図のような平行四辺形ABCDがあります。辺ADの中点をEとし、直線BEと対角線ACの交点をFとするとき,△ACDと△BCFの面積比を求めなさい。
解答と解説
試験問題1の解答:
求めたい鉛筆1本の値段をXとします。
鉛筆8本と150円のボールペン1本の代金
鉛筆8本と150円のボールペン1本の代金の合計は次の式で表すことができます。
鉛筆8本と150円のボールペン1本の代金 = 8X + 150 ・・・(1)
鉛筆2本と60円の消しゴム1個の代金
鉛筆2本と60円の消しゴム1個の代金の合計は次の式で表すことができます。
鉛筆2本と60円の消しゴム1個の代金 = 2X + 60 ・・・(2)
鉛筆8本と150円のボールペン1本の代金の合計は、同じ鉛筆2本と60円の消しゴム1個の代金の合計の3倍の合計ということなので式(1)と式(2)は次の関係が成り立ちます。
8X + 150 = 3(2X + 60)
この式を解くと求めたい、鉛筆1本の値段Xが求まります。
8X + 150 = 3(2X + 60)
8X - 6X = 180 - 150
2X=30
X=15
解答:15円
試験問題2の解答:
速度=距離÷時間
毎回同じことを書いていますが、上の公式を覚えられない人は次のような覚え方をすれば頭にはいりやすい。
バイクや車などにあるスピードメーターのを思い浮かべてください。『km/h』と表示されていると思います。これは、速度の単位で、
速度=km/h=距離/時間
のことを意味します。簡単ですね。
そして、問題を特に当たり注意しなければならないのは、単位です。設問では速度を毎時3kmや、毎時6㎞と言う表現を使っています。毎時というのは1時間単位のことを表しており、毎時3kmは1時間で3㎞すすむ、毎時6kmは1時間で6㎞進むことになります。単位としては『km』『時間(h)』を使用しています。
それに対し、所要時間は『分』、坂道の長さは『m』で表現されており、単位がことなります。違う単位どうしで計算すると間違った解答になってしまうので予め単位を合わすようにしておきましょう。
時速3㎞というのは、時速3000m(3×1000)。これで1時間あたりに進む距離が3000mと分かりました。更に時間の単位を「時間」ではなく「分」に変換する必要があります。
1時間=60分
よって、60分で3000m進むことが分かりました。1分あたりに進む距離は、50m。計算は次の通り。
1分あたりに進む距離=3000/60=50m
よって、時速3㎞というのは、分速50mになります。
同様の計算で時速6㎞というのは、分速100mになります。
さて、ここまでは単位を合わせるための計算だったのですが、ここからが公式にあてはめて設問の解答を求めていきます。
毎時6㎞の所要時間をT、求めたい坂道の長さをLとした場合、公式にあてはめると次のようになります。
毎時6kmの場合
速度=距離÷時間
100=L÷T ・・・(1)
毎時3kmの場合
速度=距離÷時間
50=L÷(T+5) ・・・(2)
ここで式(1)を式(2)に代入すると求めたい坂道の長さLを求めることができます。
100=L÷T ・・・(1)
T=L/100
式(2)へ代入
50=L÷(T+5) ・・・(2)
50(T+5)=L
50(L/100+5)=L
(L/2)+250=L
L/2=250
L=500
解答:500m
試験問題3の解答:
求めたい中央の日をNとして考えます。そうすると、囲まれた日の数字は次のように表すことができます。
中央の日:N
中央の前の日:N-1
中央の次の日:N+1
中央の上の日:N-7
中央の下の日:N+7
これらの合計が105になるので、次の式が成り立ちます。
N+(N-1)+(N+1)+(N-7)+(N+7)=105
この式を解くと中央の日Nが求まります。
N+(N-1)+(N+1)+(N-7)+(N+7)=105
5N=105
N=21
解答:21日
試験問題4の解答:
Y=aX-1 ・・・(1)
Y=-X+5 ・・・(2)
交点のX座標が2ということなので、式(2)にX座標2を代入すると交点のY座標が求まります。
Y=-X+5 ・・・(2)
Y=-2+5=3
これで交点の座標が(2、3)と分かりました。この座標を式(1)へ代入すると定数aの値が求まります。
Y=aX-1 ・・・(1)
3=2a-1
2a=4
a=2
解答:2
試験問題5の解答:
△AEFと△CBFは、相似の三角形で相似比は1:2。
何で相似なのかが分からない方は、次の相似条件をもう一度確認してください。今回の場合であれば(3)が該当しています。2組の角どころか3組の角が等しいです。
(1) 3組の辺の比が等しい
(2) 2組の辺の比が等しく、そのはさむ角が等しい
(3) 2組の角が、それぞれ等しい
よって、、AF:FC=1:2 が言えます。
なぜ、AF:FC=1:2 となるかが分からない方は、下記の二つの三角形が相似の場合、成り立つ事象を確認してください。今回は(4)が該当します。辺AEと辺BCが1:2 なので他の辺も全て1:2となります。
(4) 対応する線分の長さの比は、すべて等しい。
(5) 対応する角の大きさは、それぞれ等しい。
△ABFと△BCFの底辺をそれぞれAF、CFとした場合、高さが等しいので、△ABFの面積:△BCFの面積=1:2 となります。
また、△ACD=△ABC=△ABF+△BCFなので
△ACDの面積:△BCFの面積=(1+2):2 = 3:2
となります。
比が苦手な方は、下記のポイントでなぜ3:2になるのか分からないといういそうなので別解です。ただ、この直前までは理解できていることが前提。
△ACD=△ABC=△ABF+△BCFなので
⇓
△ACDの面積:△BCFの面積=(1+2):2 = 3:2
平行四辺形のABCDの面積を1とした場合、三角形ACDの面積は、1/2になります。また、三角形ABC=三角形ACDなので、三角形ABCの面積も1/2になります。
次に考えたいのが三角形ABFと三角形BCFの面積ですが、解説にも記載済みの通り1:2の面積比です。言い換えると、3分割した1分割分の面積が三角形ABF、残り2分割分が三角形BCFの面積となります。
これは、四角形ABCDを1/2した面積の三角形ABCを更に2/3した面積が三角形BCFの面積だということになります。計算式としては次の通り。
三角形BCFの面積=1×(1/2)×(2/3)=2/6=1/3
三角形BCFの面積は、平行四辺形ABCDの面積を1/3した面積に等しいという事です。
三角形ACDの面積は、平行四辺形ABCDの面積を1/2した面積に等しいので次の比が成り立ちます。
平行四辺形ABCD:三角形ACD:三角形BCF=1:1/2:1/3
よって、余分な平行四辺形ABCDを取り除くと次の通り。
三角形ACD:三角形BCF=1/2:1/3
分数で分かり難いので6倍して整数になおします。
三角形ACD:三角形BCF=3:2
解答:3:2

