次の問に答えなさい。
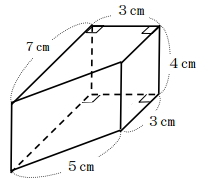
[問題1] 図のような底面が台形である四角柱の表面積は何cm²ですか。
[問題2] 時速144㎞でボールを投げたとき、18.44m先へ到達するのにかかる時間は何秒ですか。ただし、ボールの速さは一定とします。
[問題3] A市の1ヵ月の水道料金は、定額860円の基本料金と、使用量に応じて変動する従量料金の和によって算出されます。従量料金は、水の使用量が10m³以下のときは1m³につき22円、10m³を超えると超えた分は1m³につき128円に設定されています。1ヵ月の水道料金が2,872円だったとき、水の使用量は何m³ですか。ただし、消費税は考えないものとします。
[問題4] 長さが3cm、5cm、7cm、9cm、12cmのまっすぐな針金が1本ずつあります。この中から3本を選んで各々の針金を1辺とする三角形をつくるとき、三角形ができる針金の組み合わせは全部で何通りありますか。
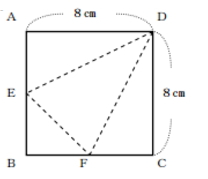
[問題5] 図のように、1辺が8cmの正方形の折り紙の頂点を各々A、B、C、Dとし、辺AB、辺BCの中点をそれぞれE、Fとします。この折り紙を線分DE、EF、FDで折り曲げて三角錐を作ります。このとき、この三角錐の底面三角形DEFに対する高さは何cmですか。
解答と解説
試験問題1の解答:
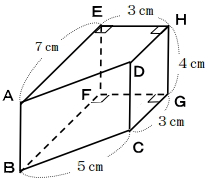
四角柱の各面の面積を一つずつ求めていきます。
四角形ABCDの面積
辺BCは、5cm、辺DCは辺HGと同じ長さなので4cm。よって、四角形ABCDの面積は次の通り。
ABCDの面積=5×4=20cm²
四角形DCGHの面積
辺CGは3cm、HGが4cmなので四角形DCGHの面積の面積は次の通り。
四角形DCGHの面積=4×3=12cm²
四角形ABFEの面積
辺AEは7cm、辺EFはHGと同じ長さなので4cm。よって、四角形ABFEの面積の面積は次の通り。
四角形ABFEの面積=7×4=28cm²
四角形EFGHの面積
辺EHは3cm、辺HGが4cmなので、四角形EFGHの面積は、次の通り。
四角形EFGHの面積=4×3=12cm²
台形AEHDの面積
辺AEの長さが7cm、辺EHが3cm、辺HDがGCと同じなので3cm。台形の面積を求める公式は『(上底+下底)×高さ÷2』。辺AEを下底、辺HDを上底として計算すると台形AEHDの面積は次の通り。
台形AEHDの面積=(7+3)×3÷2=15cm²
台形BFGCの面積
台形BFGCの面積は、台形AEHDの面積と同じなので15cm²
四角柱の表面積
よって、四角柱の表面積はこれらの各面の合計なので次の通り。
四角柱の表面積=20+12+28+12+15+15=102cm²
解答:102cm²
試験問題2の解答:
速度=距離÷時間
毎回同じことを書いているのですが、公式を覚えられない人は次のような覚え方をするとよい。
バイクや車などのスピードメーターに記載されている速度の単位を思い浮かべてください。『km/h』と表示されていると思います。これは、
速度=km/h=距離/時間
のことを意味します。簡単ですね。
この問題で注意しなければならないのは、単位です。
時速144㎞というのは、1時間あたりに進む距離が144㎞ということです。よって、この単位は時間が「時間」、距離が「km」という単位を使用しています。それに対して、ボールの到達距離は、18.44mとメートル表記。更に、求められている解答の時間は単位が「秒」となっています。
違う単位どうしで計算すると間違った解答になってしまうので予め単位を合わすようにしておきましょう。
時速144㎞というのは、時速144000m(144×1000)。これで1時間あたりに進む距離が144000mと分かりました。更に時間の単位を「時間」ではなく「秒」に変換する必要があります。
1時間=60分=3600秒
よって、3600秒で144000m進むことが分かりました。1秒あたりに進む距離は、40m。計算は次の通り。
1秒あたりに進む距離=144000/3600=40m
よって、時速144㎞というのは、秒速40mになります。
丁寧に計算しましたが、分かる人は下記の計算ですんなり求められるはずです。
144×1000÷3600=40m/s
さて、単位を合わせたので公式にあてはめて計算していきます。求めたいボールが到達する時間をSとした場合、次のような計算になります。
速度=距離÷時間
40=18.44÷S
S=18.44÷40=0.461秒
解答:0.461秒
試験問題3の解答:
水の使用量が10m³以下かそれ以上なのか?によって、計算が変わってくるのでまずはその確認を行います。(10m³を超えた場合の料金条件が設問に書かれているので、ほぼ間違いなく使用量は10m³を超えると思った方がいい)
水の使用量が10m³以下かそれ以上かを確認する
確認するには境界となる使用量10m³のときの場合を考えます。使用量が10m³の場合は、従量料金は、1m³あたり22円なので、10m³×22円=220円となる。これに基本定額料金860円が加わるので使用量10m³のときの料金は、220円+860円=1080円。1ヶ月の水道料金は2,872円ということなので、使用量10m³以上確定です。
10m³を超えた分の水の量を求めます
水の使用量10m³のときの料金は、1,080円だと分かりました。よって、1ヵ月の水道料金からこの料金を引いた値段が10m³を超える部分の水の料金になります。
10m³を超えた分の水道料金=2872-1080=1792円
10m³を超えると、1m³につき128円の料金なので、使用した水の量は次の通り。
10m³を超えて使用した水の量=1792÷128=14m³
これは10m³を超えて使用した水の量なので、これに10m³を加えると使用した水の量が求まります。
1ヵ月で使用した水の量=14+10=24m³
解答:24m³
試験問題4の解答:
『組合せ』と言う言葉を聞いてすぐに下記の組合せの公式が頭に浮かぶ人は素晴らしい。

しかし、今回はこの公式は利用しません。力技でいきます。公式を利用しても5種類の針金から3種類を選ぶ組み合わせ総数は導けますが、選ぶ針金によっては三角形にならない組み合わせが存在します。よって、結局は力技が必要になります。
5種類の針金から3種類を選ぶ場合の組み合わせは次の10通りあります。これは、順番に書き出せばすぐにでてきます。
① 3cm-5cm-7cm
② 3cm-5cm-9cm
③ 3cm-5cm-12cm
④ 3cm-7cm-9cm
⑤ 3cm-7cm-12cm
⑥ 3cm-9cm-12cm
⑦ 5cm-7cm-9cm
⑧ 5cm-7cm-12cm
⑨ 5cm-9cm-12cm
⑩ 7cm-9cm-12cm
しかし、三角形になる条件とうのがあります。
『3つの辺の内、短い2辺の合計が一番長い辺の長さよりも長くなる必要がある』
a≦b≦cのとき
a+b>c
そうすると、10種類あるなかで下記の5組が三角形として成立することになります。
① 3cm-5cm-7cm 3+5>7 OK
② 3cm-5cm-9cm 3+5>9 NG
③ 3cm-5cm-12cm 3+5>12 NG
④ 3cm-7cm-9cm 3+7>9 OK
⑤ 3cm-7cm-12cm 3+7>12 NG
⑥ 3cm-9cm-12cm 3+9>12 NG
⑦ 5cm-7cm-9cm 5+7>9 OK
⑧ 5cm-7cm-12cm 5+7>12 NG
⑨ 5cm-9cm-12cm 5+9>12 OK
⑩ 7cm-9cm-12cm 7+9>12 OK
解答:5通り
試験問題5の解答:
この問題を解くには、三角形の面積を求める公式と、三角錐の体積を求める公式を知っている必要があります。三角形の面積の公式は誰でも知っている? と思いますが、三角錐の体積を求める公式は次の通りです。
三角錐の体積=底面積×高さ÷3
三角形の面積=底辺×高さ÷2
底面を三角形DEFとした三角錐の高さを求めようとしても普通には求まらない。解き方の流れとしては、次の通り。
①三角錐の体積を別の方法で求める。
②三角錐の体積が分かれば、底面積は三角形DEFなので求めることが可能。よって、分かっている体積と、底面積を公式にあてはめると、不明な高さを求めることができます。
三角錐の体積=底面積×高さ÷3
三角錐の体積を求める
折り紙を点線通りにおると三角錐ができますが、この時、底面を三角形DEFではなく、三角形EBFを底面として考えます。点E、Fは、辺AB、BCの中点なので、BE=BF=4cmだとわかります。よって、三角形EBFの面積は次の通り。
三角形EBFの面積=4×4÷2=8cm²
次に三角錐の体積を求めるには高さが必要なのですが、三角形EBFを底面として点線で折り紙を折った場合、∠Cが直角なので辺DCが高さになります。これは、実際に点線で折り紙を折ってみるとすぐにわかります。よって、三角錐の体積は次の通り。
三角錐の体積=8×8÷3=64/3
三角形DEFを底面とした三角錐の高さを求める
まずは、三角形DEFの面積をもとめます。素直に求めてもいいのですが、これは、正方形の面積から三角形AED、三角形EBF、三角形FCDの面積を引く方が楽に求められます。
△DEFの面積=四角形ABCDの面積-△AED-△EBF-△FCD
=(8×8)-(4×8÷2)-(4×4÷2)-(4×8÷2)
=64-16-8-16
=24cm²
次に体積ですが、三角形DEFを底面にしようが、三角形EBFを底面にしようが同じ点線で折り紙を折っているので体積は同じ先程求めた64/3となります。よって、これを三角錐の体積の公式にあてはめると次の通り。
三角錐の体積=底面積×高さ÷3
64/3=24×高さ÷3
高さ=(64/3)×3÷24
=64/24
=8/3
=2(2/3)
※注意
解答を8/3で止めないように! 試験問題の用紙に事前注意事項として次のような記載があります。

公式に公表されている解答は、下記のようにどちらでもいいような解答になっていますが、問題用紙に書かれている注意事項に従った方が確実です。
![]()
ここで記載している解答は、( )をつけさせてもらっていますが、本番は、上記の通り記載してください。
解答:2(2/3)

