次の問に答えなさい。
[問題1] 大人3人と子供5人で動物園に行き、入園料として合計3,000円払いました。子供の入園料は大人の入園料の6割です。このとき、子供1人の入園料は何円ですか。ただし、消費税は考えないものとします。
[問題2] 濃度8%と濃度3%の食塩水を混ぜて、濃度6%の食塩水を300g作ります。このとき、必要な濃度8%の食塩水は何gですか。
[問題3] 黒玉4個と白玉3個が中が見えない袋に入っています。この袋から同時に2個の玉を取り出すとき、少なくとも1個が白玉である確率を求めなさい。
[問題4] 右図のような正方形ABCDがあります。ABを8cm長くし、BCを2cm短くしました。このときできる長方形A′B′C′D′の面積は、もとの正方形の面積の2倍より8cm²小さくなりました。このとき、もとの正方形の1辺の長さは何cmですか。
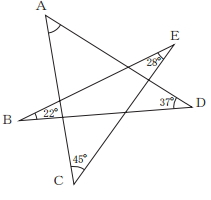
[問題5] 図のような,星形五角形ABCDEがあります。∠B=22°、∠C=45°、∠D=37°、∠E=28°のとき、∠Aは何度ですか。
解答と解説
試験問題1の解答:
大人の入園料をXとします。求めるのは子供の入園料なので、子供の入園料をXとしてもよいが、大人の入園料をXとする方が計算はしやすい。
大人の入園料
X円
子供の入園料
大人の入園料の6割なので、子供の入園料は次の通り。
X円 × 0.6 = 0.6X
大人3人の入園料
X円 × 3人 = 3X
子供5人の入園料
0.6X円 × 5人 = 3X
大人3人と子供5人の合計入園料
3X + 3X = 6X
大人3人と子供5人の合計入園料が出ました。支払った額は3,000円なので次の式が成り立ちます。
大人3人と子供5人の合計入園料 = 3,000円
6X = 3000
X=500
Xは、大人の料金であり、求めたい子供の料金は大人の料金の6割なので次の通り。
500 × 0.6 = 300
よって、求めたい子供一人の料金は、300円
解答:300円
試験問題2の解答:
[食塩水(g)]×[濃度(小数)] = 食塩(g)
公式と思ってしまうと難しく思えてしまうが、用語の意味が分かっていれば公式を覚えていなくてもこの式が頭に思い浮かべることができます。
食塩水とは?
水と塩の混合水のこと
濃度とは?
水に何%の塩が混ざっているか?
この言葉の意味を抑えて例を見て頂ければ、公式がすぐに頭に思い受べられるようになります。
例)
100グラムの食塩水がある。この食塩水の濃度は、50%(0.5)である。このような食塩水がある場合、公式を知らなくても100グラムの内、50%の50グラムが水、残り50グラムが塩だとすぐに頭に浮かびますよね? あなたが頭の中で瞬時にした計算は次だと思います。
100 × 0.5 = 50
結局これが公式と同じ計算をしていることになります。
100 × 0.5 = 50
↓
[食塩水(g)]×[濃度(小数)] = 食塩(g)
これさえ頭に入れておけば、濃度算の問題は難しくありません。
それでは問題をといていきます。まずは、今回の問題を図にしたものが下図です。
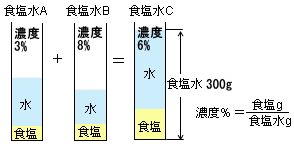
求めたい濃度8%の食塩水をXgとします。
食塩水Bについて考える。
濃度8%の食塩水
Xグラム ・・・(1)
濃度8%の食塩
食塩水がXグラム、濃度が8%なので食塩の量は、
X × 0.08 = 0.08Xグラム ・・・(2)
食塩水Aについて考える。
濃度3%の食塩水
濃度8%と3%との合計グラム数が300グラムなので、濃度3%の食塩水の量は次の通り。
300-X グラム ・・・(3)
濃度3%の食塩
食塩水が300-Xグラム、濃度が3%なので食塩の量は、
(300-X) × 0.03 = 9-0.03X グラム ・・・(4)
食塩水Aと食塩水Bの混合水について考える。
濃度6%の食塩水
食塩水の量は、設問より300グラムと分かっている。
濃度6%の食塩
食塩の量は、濃度が6%なので次の通り。
300×0.06=18 グラム
混合水の塩の量が18グラムと分かりました。これは、食塩水Aの塩と食塩水Bの塩の量を足した値と等しいはずなので式(2)(4)より、次の式が成り立ちます。
0.08X + (9-0.03X) = 18
この式を解くと、求めたい濃度8%の食塩水をXが求まります。
0.08X + (9-0.03X) = 18
0.05X=9
X=180 グラム
解答:180g
試験問題3の解答:
組合せの公式を利用する必要があります。

本来であれば、少なくとも1個が白玉である確率を求めるには次の式になる。
少なくとも1個が白玉である確率=
(少なくとも1個が白玉である組合せ数)/(7個から2個を選ぶ組み合わせ数)
しかし、分子の『少なくとも1個が白玉である組合せ数』を出すことは困難。よって、発想の転換をする。『少なくとも1個が白玉がでる』というのは、『2つとも黒玉である』の反対の意味である。よって、2つとも黒玉がでる組合せ数をもとめ、更にここから2つとも黒玉がでる確率を求めます。
もし、2つとも黒玉がでる確率が20%(1/5)の確率であれば、『少なくとも1個が白玉がでる』確率は逆の80%(4/5)ということになる。
黒玉4個と白玉3個の合計7個から同時に2個取り出す場合の組み合わせ総数は、次の通り。
7C2=(7×6)/(2×1)=42/2=21 通り
2つ選んだ玉が両方黒玉のパターン数は
4C2=(4×3)/(2×1)=6 通り
よって、両方黒玉になる確率は、
6÷21=2/7
よって、『少なくとも1個が白玉がでる』確率は、両方黒玉になる確率の逆なので次の通り。
1-2/7=5/7
解答:5/7
試験問題4の解答:
元の正方形の1辺の長さをXとします。
元の正方形ABCDの面積は次の通り。
X × X = X²
長方形形A′B′C′D′の面積は次の通り。
(X+8) × (X-2) = X²+6X-16
長方形形A′B′C′D′の面積は元の正方形ABCDの面積の2倍より8cm²小さいという事なので次の式が成り立ちます。
X²+6X-16 = X² × 2 -8
この式を解くと求めたい元の正方形の1辺の長さXが求まります。
X²+6X-16 = X² × 2 -8
X²+6X-16 = 2X² -8
X²-6X+8 =0
(X-4)(X-2)=0
X=4、2
ここでXは4cmと2cmと2つ解が出たが2cmの場合、設問にある正方形を長方形に変形させる際の『BCを2cm短くしました。』を行うと0cmになってしまい長方形が成り立たなくなるので2cmは不可。
よって、求める解答は4cmのみとなる。
この問題は少し不親切なところがある。
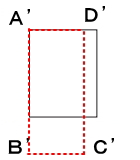
設問通り、辺ABを8cm伸ばし、BCを2cm短くしようとすると下図のようになる。
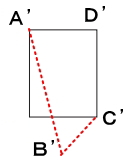
しかし、問題内には記載されていませんが、ABを8cm伸ばす際にDCも同時に8cm伸ばす。更にBCを2cm縮める際にADも同時に2cm縮めて下図の様にしなければならない。これは『長方形A′B′C′D′』という文面から読み取るしかない。上図の場合、長方形にはならない。
解答:4cm
試験問題5の解答:
下図の①から順に角度を求めていくことで∠Aを求めることができます。
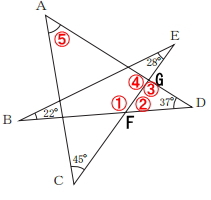
①の角度を求める
∠B=22° 、∠E=28°
よって、
①の角度=180-22-28=130°
②の角度を求める
①が130°なので
②の角度=180-130=50°
③の角度を求める
∠D=37°、②の角度=50°
よって、
③の角度=180-37-50=93°
④の角度を求める
③が95°なので
④の角度=180-93=87°
⑤の角度を求める
∠C=45°、④の角度=85°
よって、
⑤の角度=180-45-87=48°
解答:48°

