次の問に答えなさい。

[問題1]ある学校の男子生徒数は女子生徒数より24人多く、全校生徒の55％が男子です。このとき、この学校の全生徒数は何人ですか？

[問題2]Ａ地点とＢ地点を往復します。Ａ地点からＢ地点まで2,200ｍあり、行きは15分走って23分歩き，帰りは10分走って30分歩きました。このとき、歩く速さは分速何ｍですか？

[問題3]２つのサイコロを同時に投げるとき、 出た目の数の和が４の倍数になる確率を求めなさい。

[問題4]容器Ａには、濃度4％の食塩水、容器Ｂには、濃度7.5％の食塩水が入っています。2つの食塩水すべて混ぜ合わせると、濃度5％の食塩水が350ｇできました。容器Ａには、初め食塩水が何ｇ入っていましたか？

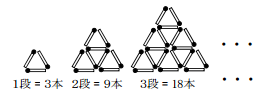東京 職業訓練問題[[問題5]右図のように、正三角形に並べたマッチ棒を、１段、２段、･･･と並べて大きな正三角形をつくります。１段をつくるには３本、２段をつくるには９本のマッチ棒が必要となります。この規則にしたがって15段の正三角形をつくるとき、必要なマッチ棒は何本ですか？

解答と解説

試験問題１の解答：
求めたい学校の全生徒数をＮ人とします。

全校生徒の55％が男子ということより、男子生との数は次の式で表すことができます。
　男子生徒数 ＝ Ｎ x 0.55 ・・・（１）

更に女子生徒数は、男子生徒数より24人少ないということより、女子生徒の数は次の式で表すことができます。
　女子生徒数 ＝ (Ｎ x 0.55) – 24 ・・・（２）

この男子生徒数（１）と、女子生徒数（２）を足した数が全生徒数Ｎになるので、全生徒数Ｎは次の式で表すことができます。
　全生徒数Ｎ ＝ (Ｎ x 0.55) + (Ｎ x 0.55) – 24
　　　　　Ｎ ＝ 0.55Ｎ + 0.55Ｎ – 24
　　　　　Ｎ ＝ 1.1Ｎ – 24
　　　　　Ｎ – 1.1Ｎ ＝ -24
　　　　　0.1Ｎ ＝ 24
　　　　　Ｎ ＝ 240人

よって、求める全生徒数Ｎは、240人となる。

解答：240人

試験問題２の解答：
速度、距離、時間を求めるには下記の公式を知っておく必要があります。3つとも同じ公式で、形を変えているだけです。よって、いずれか1つを覚えておいて、変形できるようにだけしておけばよい。

　速度 ＝ 距離 ÷ 時間
　距離 ＝ 速度 x 時間
　時間 ＝ 距離 ÷ 速度

歩く速度をＷm/分、走る速度をＶm/分とします。

●Ａ地点⇒Ｂ地点の往路
　歩いた距離 ＝ Ｗ x 23 ＝ 23Ｗ
　走った距離 ＝ Ｖ x 15 ＝ 15Ｖ

　歩いた距離と走った距離の合計は2,200mなので次の式が成り立ちます。
　23Ｗ + 15Ｖ ＝ 2,200 ・・・（１）

●Ｂ地点⇒Ａ地点の復路
　歩いた距離 ＝ Ｗ x 30 ＝ 30Ｗ
　走った距離 ＝ Ｖ x 10 ＝ 10Ｖ

　歩いた距離と走った距離の合計は往路と同じなので2,200m。
　30Ｗ + 10Ｖ ＝ 2,200 ・・・（２）

式（１）（２）の式を解くことで求めたい、歩く速さを算出することができます。

　23Ｗ + 15Ｖ ＝ 2,200 ・・・（１）
　30Ｗ + 10Ｖ ＝ 2,200 ・・・（２）

式（１）の両辺に2を、式（２）の両辺に3を掛けます。すると2式は下記の様になります。

　46Ｗ + 30Ｖ ＝ 4,400 ・・・（１）
　90Ｗ + 30Ｖ ＝ 6,600 ・・・（２）

式（２）から式（１）を引くと

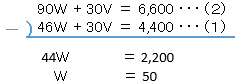
東京都 試験問題

よって、求める解答は、分速50m。

解答：分速50m

試験問題３の解答：
2つのサイコロの出た目の数の和が4の倍数になるということは、和が4、8、12のいずれかになるということです。

確率を求めるには次の計算式を覚えておく必要があります。

職業訓練 確率

また、ここで言うパターン数というのは組み合わせ数の事を意味します。更に組み合わせ数を求めるには次の公式が必要になります。

職業訓練 公式

●サイコロ2つを振ったさいの出る目の組み合わせ総パターン数を求める
1つのサイコロから出るパターン数は、1～6の6種類。これが2つあるので、サイコロ2つを振ったさいの出る目の組み合わせ総パターン数は、6ｘ6＝36パターンある。

●求めたいパターン数を求める
ここで言う求めたいパターン数というのは、2つのサイコロの目の和が4、8、12になる組み合わせの数のことです。

  • 目の和が4になるのは、(1,3)、(3,1)、(2,2)の3通り
  • 目の和が8になるのは、(2,6)、(6,2)、(3,5)、(5,3)、(4,4)の5通り
  • 目の和が12になるのは、(6,6)の1通り

よって、2つのサイコロの目の和が4、8、12になる組み合わせの数は、全部で9通りとなります。

これを確率の公式に当てはめると、

　確率 ＝ 9 ÷ 36 ＝ 1/4 あるいは、0.25

よって、2つのサイコロの出た目の数の和が4の倍数になる確率は、1/4(あるいは、0.25)

解答：1/4(あるいは、0.25)

試験問題４の解答：
求めたい容器Ａの食塩水の量をＮグラムとします。食塩水の合計が350gということより、容器Ｂの食塩水の量は、350-Ｎと表すことができます。

　容器Ａの食塩水の量： Ｎ
　容器Ｂの食塩水の量： 350-Ｎ

更に容器Ａの食塩水の濃度は４％、容器Ｂの食塩水の濃度は7.5％、合計すると5％の濃度になるということより、

　容器Ａの食塩量：Ｎｘ0.04 ＝ 0.04Ｎ ・・・（１）
　容器Ｂの食塩量：(350-Ｎ)ｘ0.075 ＝ 26.25-0.075Ｎ ・・・（２）
　合計の食塩量：350ｘ0.05 ＝ 17.5 ・・・（３）

容器Ａの（１）と容器Ｂの（２）を足すと（３）の食塩量になるということより、次の式で表すことができます。

　0.04Ｎ + 26.25-0.075Ｎ ＝ 17.5
　-0.035Ｎ ＝ -8.75
　Ｎ ＝ 250

よって、求める解答は、250g。

解答：250g

試験問題５の解答：
規則性を見つけられるかが重要。そして、見つける為にはまずは書き出すことが大切です。書き出すことで見えてくる場合があります。例えば今回の場合、下記のように書き出すと、？？のところに何がくるか想像できますでしょうか？

　1段に必要な数：3本(+3)
　2段に必要な数：9本(+6)
　3段に必要な数：18本(+9)
　4段に必要な数：??本(+??)

+3、+6、+9ときているので、+12がくることが分かりますね。よって、4段目は30本(+12)となる。このまま力ずくで15段まで行ってもよいが時間がかかるので、できる限り要領よく解くようにしましょう。

よく見ていると別の法則も見えてきます。段数x3 ずつマッチの数が増えて行っているということです。よって、14段から15段では45本増えることになります。増分だけなら次のようになります。

　+3、+6、+9、+12、・・・・+45

この増分を全て足した数がマッチ棒の総数になります。

　1段に必要な数：3本(+3) ⇒ +3
　2段に必要な数：9本(+6) ⇒ +3+6=9
　3段に必要な数：18本(+9) ⇒ +3+6+9=18
　4段に必要な数：??本(+??) ⇒ ・・・

よって、「+3、+6、+9、+12、・・・・+45」を合計すればマッチの総数が出るのですが、ここでも単純に力技で合計するのではなく、等差数列の和の公式といものを使用します。一見難しいように思えるのですがいたって簡単です。下記の例を見て頂ければわかると思います。

等差数列の和の公式 例
下記の様に1～6までの等しい間隔の数値が並んでいる場合、に使用できる合計を求める公式。

　1、2、3、4、5、6

普通に足しても簡単に合計が求められますが、一番先頭の1と最後の6を足すと7になります。同様に前から2番目の数と、後ろから2番目の数を足すと7になります。このように等間隔で並んでいる数値の場合、前からと後ろから順番に１つずつ数値をピックアップし、足すと全てが同じ数になります。

　1+6=7
　2+5=7
　3+4=7

といったように全て7になります。そして、その7ができる数は、数値の数の半分になる。上記例であれば、1～6の6つの数がある。その半分の3ができる数です。前後の数を足して作っているので、できる数が半分になるのは当然ですよね。

そうすると1～6の数値の合計は7ｘ3＝21だと分かります。この程度なら１つずつ足しても簡単なのであまり、ありがたみが分かりませんが、下記の様に1～100だったらどうでしょう？さすがに1つずつ足せませんよね。

　1、2、3、4、5、6・・・95、96、97、98、99、100

この場合も同様の考え方です。前後の数を足すと、1+100＝101となります。これが100÷2＝50個できることになるので、1～100の合計は、

　101ｘ50＝5050

と直ぐにわかります。

では、本題の「+3、+6、+9、+12、・・・・+45」ですが、もう簡単ですよね。15段なので数の種類(+3、+6、+9、+12、～ +45)は15あることになります。 前後の合計は、48となりこれが15÷2あることになるので、合計は、

　48ｘ(15/2)＝360

よって、求める解答は360本となります。；

解答：360本