次の問に答えなさい。
[問題1] YはXに比例し、X=-3のときY=30となります。X=-6のときYの値を求めなさい。
[問題2] 1秒間に一度分裂を起こして2つになる細胞があります。生まれた細胞も分裂を繰り返していきます。細胞の数が2048個となるのは何秒後ですか。
[問題3] 図は点Oを対称の中心とする点対称な図形です。頂点Aに対応する頂点はどれですか。
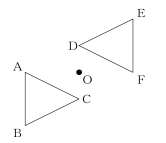
[問題4] 正十七角形の内角の和は何度ですか。
[問題5] 図のように、直線Y=2X+4があり、X軸との交点をBとします。直線状の任意の点AからX軸に下ろした垂線とX軸との交点をHとするとき、線分AHの中点CとBを結ぶ直線の式を求めなさい。
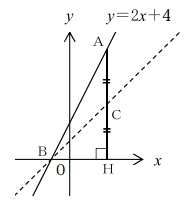
解答と解説
試験問題1の解答:
YはXに比例すということなので、比例係数をaとすると、YとXの関係は次の式で表すことができます。
Y=aX
X=-3のときY=30ということなので、上の式にYとXの値を代入しaの値を求めます。
30=a×(-3)
-3a=30
a=-10
よって、YとXの関係式は次のようになります。
Y=-10X
これでX=-6のときのYの値を求めることができます。
Y=-10X
=-10×(-6)
=60
解答:60
試験問題2の解答:
1個の細胞が1秒後には総数2個、2秒後には総数4個、3秒後には8個、4秒後には16個と増えていきます。1秒経過するごとに、『1、2、4、8、16・・・』増えていく増え方は、経過秒数をnとした場合、2nに相当します。
求めたいのはこの2nが2048となるようなnの値です。よって、次の式が成り立ちます。
2n=2048
n=11
nは、対数logを使用して求めることもできますが、ここでは、力ずくで2を何回掛ければ2048になるか? といったように実際に2を掛けていき回数を求める方が早くて確実。
解答:11秒後
試験問題3の解答:
点Oが対象点なので頂点Aの対象となる点は頂点Fとなります。
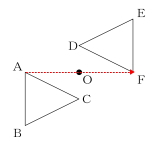
解答:頂点F
試験問題4の解答:
内角の和を求めるにあたり必ず知っておく必要があるのが、三角形の内角の和です。三角形の内角の和は、180°で、これは今回の問題だけではなく様々な問題で使う場面が出てくるので必ず覚えておきましょう。
多角形の内角の和を求める方法は、その多角形に三角形がいくつ含まれるかを考えます。例えば、四角形の場合であれば、図のように2つの三角形ができます。よって、内角の和は180×2=360°となります。
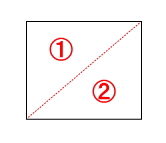
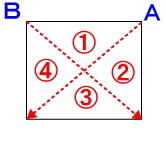
三角形を作る際の注意点として、必ず1点から線を引くこと。下図のようにA点、B点の2ヵ所から線を引いて三角形が4つできた! 180×4=720° としないように。
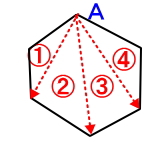
更に例として、下図のように6角形の場合であれば点Aの一カ所から各頂点に線を引いてできる三角形の数を数えます。そうすると、4つの三角形ができるので6角形の内角の和は、次のようになります。
180×4=720°
さて、本題ですが設問は正十七角形の内角の和を求められています。『正』は意識する必要はありません。正十七角形も普通の十七角形も内角の和は一緒です。しかし、十七角形ともなると上記で記載した例のように図を描いて三角形の数を数えるのも大変です。そこで、覚えておきたいのが簡単な公式です。
N角形に含まれる三角形の数は、次の式で表すことができます。
N角形に含まれる三角形の数=(N-2)個
よって、十七角形の場合、できる三角形の数は、15個とわかります。
17-2=15個
よって、十七角形の内角の和は、次の通りです。
180×15=2700°
解答:2700°
試験問題5の解答:
あまり難しく考える必要はない。
まず、B点を通るのは分かっているので、そのB点の座標はY=2X+4の直線がX軸と交わるところなのでY=0となるところです。
Y=2X+4
0=2X+4
X=-2
よって、B点の座標は(-2、0)と分かります。
更に、点Aは直線Y=2X+4の任意の場所なので直線状であればどこでもよい。よって、一番分かりやすいのが下図のようにY軸と交わるところをA点として考える場合です。Y軸との交点は、直線Y=2X+4の切片なので(0、4)と即分かります。
また、点Cは、AHの中点なのでその座標は、(0、2)になります。よって、求めたい直線は、点B(-2、0)と点C(0、2)の2点を通る式になります。
直線の式は、
Y=aX+b
であらわすことができます。そして、Y軸との交点が点C(0、2)なので求める直線の切片bは2となります。
Y=aX+2
更に点B(-2、0)と点C(0、2)を通るのでどちらかの点の座標を上記式に値を代入するとaの値も求まり、直線の式が出てきます。
点B(-2、0)を代入
Y=aX+2
0=-2a+2
a=1
よって、求める直線の式は次の通り。
Y=X+2
解答:Y=X+2

