次の問に答えなさい。
[問題1] ある商品は原価の4割増しの定価が設定されています。この商品を60円安く販売したところ、利益は300円になりました。このとき、商品の定価は何円ですか。ただし、消費税は考えないものとします。
[問題2] 1時間に0.3リットルずつ消費すると,40時間で無くなる燃料があります。この燃料を24時間で使い切るには、1時間に何リットルずつ消費するとよいですか。
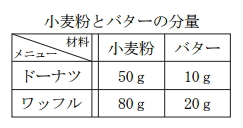
[問題3] 表は,ドーナツとワッフルを1個ずつ作るのに必要な小麦粉とバターの分量を表したものです。この分量に従いドーナツとワッフルをそれぞ
れ数個作ったところ,小麦粉1,110gとバター250gを使用しました。このとき、できたドーナツは何個ですか。
[問題4] A,B,C,D,E,Fの6人がいます。この6人が横1列に並ぶとき、AとFが隣どうしになる並び方は全部で何通りありますか。
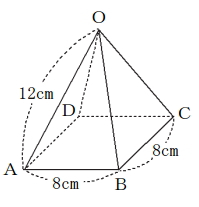
[問題5] 図のような正四角すいOABCDがあります。底面ABCDは、1辺の長さが8cmの正方形で、他の辺の長さはすべて12cmです。この正四角すいの表面積は何cm²ですか。
解答と解説
試験問題1の解答:
原価をX円と仮定します。(求めたい定価をX円と仮定して計算してもよいが、原価をX円として計算する方が計算は容易)
定価は、原価を4割増しした価格なので次の式が成り立ちます。
定価=原価 × 1.4=1.4X
この定価1.4Xの商品を60円安く販売するということなので、その売値は次の通り。
売値=1.4X-60
その際の利益は300円ということなので次の式が成り立ちます。
利益=売値-原価
300=(1.4X-60)-X
この式を解けば原価Xが求まります。
300=(1.4X-60)-X
300=0.4X-60
0.4X=360
X=900
これで原価の価格が900円と分かりました。よって、求めたい定価は次の通り。
定価=1.4X
=1.4×900
=1,260円
解答:1,260円
試験問題2の解答:
1時間で0.3リットルずつ消費した場合、40時間で無くなるということなので、その燃料の量は次の通り。
燃料の量=0.3 × 40=12リットル
燃料の量が12リットルと分かりました。これを24時間で使い切るためには、
12リットル ÷ 24時間 = 0.5
1時間あたり0.5リットル消費すればいいことが分かります。
解答:0.5リットル
試験問題3の解答:
作ったドーナツの個数をX個、ワッフルの個数をY個と仮定します。
小麦粉に焦点を合わせて考える
ドーナツ1個作るのに使用する小麦粉の量は50g、よって、ドーナツX個を作った際に使用する小麦粉の量は、
ドーナツX個を作った際に使用する小麦粉の量=50X
ワッフル1個作るのに使用する小麦粉の量は80g、よって、ワッフルY個を作った際に使用する小麦粉の量は、
ワッフルY個を作った際に使用する小麦粉の量=80Y
また、ドーナツX個とワッフルY個を作った際に使用した小麦粉の量は設問より1,110gだと分かっているので次の式が成り立ちます。
50X+80Y=1110 ・・・(1)
バターに焦点を合わせて考える
ドーナツ1個作るのに使用するバターの量は10g、よって、ドーナツX個を作った際に使用するバターの量は、
ドーナツX個を作った際に使用するバターの量=10X
ワッフル1個作るのに使用するバターの量は20g、よって、ワッフルY個を作った際に使用するバターの量は、
ワッフルY個を作った際に使用するバターの量=20Y
また、ドーナツX個とワッフルY個を作った際に使用したバターの量は設問より250gだと分かっているので次の式が成り立ちます。
10X+20Y=250 ・・・(2)
作ったドーナツの個数を求める
式(1)(2)を解くと求めたいドーナツの個数が出てきます。
50X+80Y=1110 ・・・(1)
10X+20Y=250 ・・・(2)
式(2)の左辺、右辺を4倍した後、(1)-(2)を行います。
50X+80Y=1110 ・・・(1)
40X+80Y=1000 ・・・(2)
——————————-
10X=110
X=11
よって、作ったドーナツの個数は、11個
解答:11個
試験問題4の解答:
AとFが隣り合うので(A、F)を1セットで考えます。仮に、(A、F)の1セットを新たなGとして置き換えます。
そうした場合、B、C、D、E、G の5つが取り得る並び方の総数は、
5!=5×4×3×2×1=120通り
また、Gは、先述した通りA、Fを1セットにしたもの。このAとFの取り得る並び順は、AFとFAの2通り。よって、取り得る総組合せ数は、
120通り × 2通り = 240通り
解答:240通り
試験問題5の解答:
表面積は、底面ABCDの面積と、4つの二等辺三角形の面積を求めればよい。4つの二等辺三角形はいずれも同じ大きさなので1つの面積を求めて4倍すればよい。
底面ABCDの面積を求める
底面ABCDは、1辺が8cmの正方形なのでその面積は、
底面ABCDの面積=8×8=64cm²
二等辺三角形の面積を求める
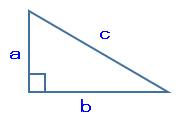
三平方の定理を知っている必要があります。下図のような直角三角形がある場合、次の式が成り立ちます。
a²+b²=c²
二等辺三角形OABに焦点を合わせて考えてみます。頂点Oから辺ABに垂直に下ろした点をEとします。そうすると辺AEの長さは4cmとわかります。三平方の定理より、辺OEの長さは、
OE²+AE²=OA²
OE²+4²=12²
OE²+16=144
OE²=128
OE=√128
OE=√64×2
OE=√8²×2
OE=8√2
これで二等辺三角形OABの高さが8√2と分かりました。よって、二等辺三角形OABの面積は次の通り。
二等辺三角形OABの面積=AB×OE÷2=8×8√2÷2=32√2
よって、2等辺三角形4つの表面積は次の通り。
2等辺三角形4つの表面積=32√2 × 4 =128√2
よって、求めたい表面積は、2等辺三角形4つの表面積と底面ABCDの面積を足した値なので次の通り。
求めたい表面積=64+128√2
解答:64+128√2