次の計算をしなさい。ただし,(5),(6)は小数で,(7)は分数で求めなさい。
[問題1] 41+507=
[問題2] 673-48=
[問題3] 26x99=
[問題4] 948÷79=
[問題5] 2.3+36.2=
[問題6] 3.3×2.6=
[問題7]
![]()
[問題8]
![]()
[問題9] 2a⁵b²c⁴÷4a⁴b³c⁴x8a³b³c²=
[問題10] x²+8x-33=0 のとき、x(x≧0)の値を求めなさい。
解答と解説
試験問題1の解答:548
試験問題2の解答:625
試験問題3の解答:2574
試験問題4の解答:12
試験問題5の解答:38.5
試験問題6の解答:8.58
試験問題7の解答:
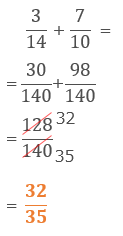
試験問題8の解答:
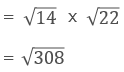
しかし、このままで終わってはいけない。問題用紙の最初のページにも下記の様な注意事項の記載がある。このままだと、せっかく分かっていても採点はXとなってしまいます。
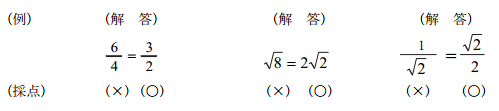
ルートから出せるものは出すようにしましょう。
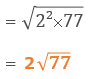
試験問題9の解答:
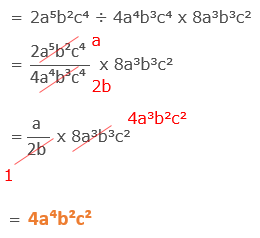
試験問題10の解答:3
この問題は、因数分解ができないと説くことができない。因数分解はしっかりとけるようにしておきましょう。
足して8、掛けて―33になる二つの数値を探す。探す方法のポイントとしては、足して8になる数よりも、掛けて-33になる2つの数値を探した方が組み合わせの数が少なく容易。掛けて33になるのは、1と33、もしくは3と11しかない。あとは、-33となるためにどちらかの数値にマイナスを付ければいいのですが、それは、足して8になる組み合わせで考えればよい。
そうするとおのずと、2つの数値は、-3と11というのが分かる。よって、因数分解すると、
(x-3)(x+11)=0
となる。よって、Xは、3と-11となる。設問よりXは、x≧0の値なので、解答は3。
※解説の内容が不明、不十分というのがあればコメントをください。

