次の問に答えなさい。

[問題1]あるクラスの男子は女子より4人少なく、クラスの45％が男子です。このクラスの男子は何人ですか？

[問題2]2種類のアメＡとＢがあります。Ａのアメ1個の重さは25g、Ｂのアメ1個の重さは30gです。ＡとＢのアメを合わせて14個、390g買いました。このとき、Ａのアメは何個買いましたか？

[問題3]1組のトランプ52枚の中から1枚ず続けて2回ひきます。このとき、ひいた2枚のカードがともにクローバーである確率を求めなさい。ただし、ひいたカードはもとに戻さないものとします。

[問題4]1辺10cmの正方形があります。この正方形の横の長さをｘ％縮め、縦の長さを2x％伸ばして長方形にします。できた長方形の面積が、もとの正方形の面積より12.5％大きくなるとき、ｘはいくつですか？

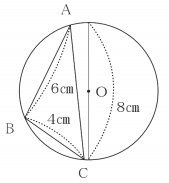東京職業訓練[問題5]右図のように円Ｏに内接する三角形ＡＢＣがあります。円Ｏの直径が8cm、ＡＢ＝6cm、ＢＣ＝4cmのとき、∠ＢＡＣは何度ですか？

解答と解説

試験問題１の解答：
求める男子の人数をＮ人とする。

クラスの男子は女子より4人少ないということより、
　男子の数は、Ｎ人
　女子の数は、Ｎ+4人

また、クラスの45％が男子ということより、
　クラスの人数、Ｎ+(Ｎ+4)＝2Ｎ+4
　Ｎ ＝ 0.45ｘ(2Ｎ+4)
　Ｎ ＝ 0.9Ｎ+1.8
　0.1Ｎ＝1.8
　Ｎ＝18人

よって、求める解答は、１８人

解答：18人

試験問題２の解答：
求めるＡのアメの個数をＮ個とします。

ＡとＢのアメを合わせて14こ購入したということなので、次のことが言えます。
　Ａのアメの個数：Ｎ
　Ｂのアメの個数：14-Ｎ

次に、Ａのアメ1個の重さ25g、Ｂのアメ1個の重さ30g、合わせて390g買ったという事なので次のことが言えます。
　(Ｎｘ25)+(14-Ｎ)ｘ30＝390

よって、この式を解くとＡのアメの個数が出てきます。
　25Ｎ+420-30Ｎ＝390
　5Ｎ＝30
　Ｎ＝6

Ａのアメの個数は6個となる。

解答：6個

試験問題３の解答：
確率は、次の公式のように求めたいパターン数を全パターン数で割るというのが基本的な考え方になります。サイコロなどで考えれば分かり易いと思います。サイコロを1回振って1が出る確率は、全パターン数は6種類、求めたいパターン数は1の1種類なので、確率は1/6となります。

　職業訓練 確率

しかし、今回のような問題は確率の公式を知っているだけでは解けない。サイコロの例のように簡単なパターン数であればすぐわかるが、全パターン数、求めたいパターン数、ようは組み合わせを求める公式を知っておく必要がある。

　職業訓練 公式

では、確率を求める為に52枚の中から2枚の抜き出す。これは組み合わせの公式を使う。

　組合せ

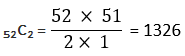
これが52枚から2枚を抜き出す全パターン数で、確率の分母となる。次に、求めたいパターン数を考えます。求めたいパターン数は、クローバーのカードの中から任意の2枚を抜き出す組合せになる。スペードのカード数は52÷4＝13枚。よって、13枚から2枚を抜き出す組み合わせは次の通り。

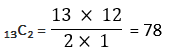
組み合わせ数

これが確率の分子となる。よって、求めたいひいた2枚のカードがともにクローバーである確率は、次の通り。

　分数計算

試験問題解答

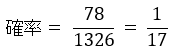
試験問題４の解答：
1辺10cmの正方形の面積は、10cmx10cm＝100cm²

この正方形の横の長さをＸ％縮め、縦の長さを2Ｘ％伸ばすので、長方形の1辺の長さと面積は次の通りになる。

まず、横の長さに関して、縮める長さは元の長さ10cmのＸ％。よって、縮める長さは、(10 × Ｘ)cmとなる。この縮める長さを元の10cmから引けば、長方形の横の長さが分かる。

　横の長さ：10 – (10 x Ｘ) ＝ 10 – 10Ｘ ・・・(１)

次に、縦の長さに関して、伸ばす長さは元の長さ10cmの2Ｘ％。よって、伸ばす長さは、(10 × 2Ｘ)cmとなる。この伸ばす長さを元の10cmに足せば、長方形の縦の長さが分かる。

　縦の長さ：10 + (10 x 2Ｘ) ＝ 10 + 20Ｘ ・・・(２)

(１)(２)より、長方形の面積は次の通りになる。

　この長方形の面積：(10 – 10Ｘ) x (10 + 20Ｘ) ・・・(３)

更に正方形の面積より、長方形の面積の方が12.5％大きいという事なので、正方形の面積100cm²と、正方形の面積100cm²の12.5％の大きさ(100 × 0.125)を、加えた面積100 + (100 x 0.125)が(３)の長方形の面積と等しくなることがいえる。

　正方形の面積 ＋ 正方形の面積の12.5％の面積 ＝ 長方形の面積

　100 + (100 x 0.125) = (10 – 10Ｘ) x (10 + 20Ｘ)
　112.5 = 100 + 200Ｘ – 100Ｘ – 200Ｘ²
　200Ｘ² – 100Ｘ + 12.5 = 0
　2000Ｘ² – 1000Ｘ + 125 = 0
　16Ｘ² － 8Ｘ + 1 = 0
　(4Ｘ-1)² = 0

よって、
　Ｘ ＝ 1/4 ＝ 0.25 ＝ 25％

解答：25

試験問題５の解答：
この問題は、正弦定理の公式を使う問題。知っていれば簡単に解けますが、知っていないと解けない問題です。

下図の様に三角形ＡＢＣに外接する円がある場合、

正弦定理

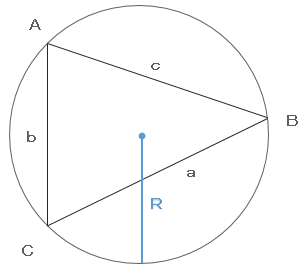
正弦定理と呼ばれる次の式が成り立ちます。

　正弦定理

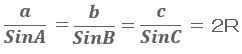
今回の問題であれば、∠ＢＡＣを求める問題なので、向かい合う辺の長さは、4cm。更に直径が8cmの円なので半径Ｒは4cmとなる。よって、正弦定理に当てはめると次のようになります。

　正弦定理

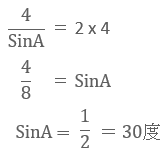
よって、求める解答は、30度。

解答：30度