問1~3に関しては以下のページに解説をまとめているので参考にして下さい。
図のように、放物線y=kx²上に、2点A、Bがあり、点Aのx座標は-4である。点Aと点Bのx座標の比は2:1 で、直線ABとy軸との交点をCとする。以下の問いにア~オから選んで答えなさい。
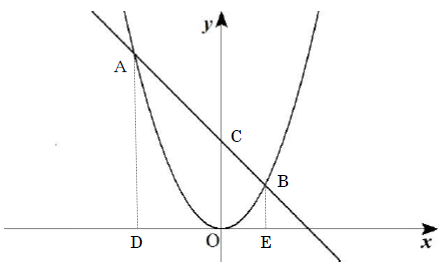
[問題1] 点Aからx軸に垂線を引き、交点をDとし、点Bからx軸に垂線を引き、交点をEとする。このとき四角形ABEDの面積をk を用いて表しなさい。
[解答群]
ア 4k イ 16k ウ 20k エ 40k オ 60k
[問題2] K=1/2のとき、△OACの面積を求めなさい。
[解答群]
ア 2 イ 4 ウ 6 エ 8 オ 10
解答と解説
試験問題1の解答:オ
点A、点B、点C、点Dの座標をそれぞれ求めていきます。
点Aの座標
点Aのx座標は-4なので、y座標は次の通り。
y=kx²
=k(-4)²
=16k
点A(-4,16k)
点Dの座標
点Aからx軸に垂線を下した点が点Dなので、x座標は-4となります。よって、点Dの座標は次の通り。
点D(-4,0)
点Eの座標
点Aと点Bのx座標の比は2:1ということなので、点Dと点Eのx座標の比も2:1になります。よって、点Dのx座標は-4なので、点Eは2だと分かります。比率はマイナス、プラスは無視します。
点E(2,0)
点Bの座標
点Eのx座標が2なので、点Bのx座標も2だと分かります。よって、点Bの座標は次の通り。
y=kx²
=k(2)²
=4k
点B(2,4k)
面積を求める
座標より、AD間の長さが16k、DE間の距離が6、BE間の距離が4kだと分かりました。四角形ABEDは下底がAD、上底がBE、高さがDEとなる台形です。よって、台形の面積を求める公式を使って面積を求めることができます。
台形の面積=(上底+下底)x高さ÷2
=(4k+16k)x6÷2
=20kx3
=60k
試験問題2の解答:エ
この問題はまともに△OACを求めようとするのではなく、四角形ADOCの面積から三角形ADOの面積を引く流れで行うと楽に面積が求められます。
四角形ADOCの面積
四角形ADOCの面積を求めるには点Cの座標を知る必要があります。k=1/2ということなので、今わかっている各点の座標は次の通り。
点A(-4,8)
点B(2,2)
点D(-4,0)
点E(2,0)
点O(0,0)
次に直線ABの式を求めていきます。直線の傾きをa、y軸との交点をbとすると直線は次の式で表すことができます。
y=ax+b
更にこの直線は、点Aと点Bを通るので各値を代入します。
点A(-4,8)を代入
y=ax+b
8=-4a+b ・・・(1)
点B(2,2)を代入
y=ax+b
2=2a+b ・・・(2)
式(1)(2)からy軸との交点であるbの値を求めます。
8=-4a+b ・・・(1)
2=2a+b ・・・(2)
式(2)の両辺に2を掛けます。
8=-4a+b ・・・(1)
4=4a+2b ・・・(2)
この式(1)(2)の左辺どうし、右辺どうしを足し算します。
(8+4)=(-4a+b)+(4a+2b)
12=3b
b=4
よって、B点の座標は(0,4)
問題1と同様に台形ADOCの面積を求めます。
台形の面積=(上底+下底)x高さ÷2
=(4+8)x4÷2
=12×2
=24
次に三角形ADOの面積を求めます。
三角形ADOの底辺DOの長さは4、高さADの長さは8なので面積は次の通り。
三角形ADOの面積=4×8÷2
=16
三角形OACの面積は次の通り。
三角形OACの面積=台形ADOCの面積-三角形ADOの面積
三角形OACの面積=24-16=8
※解説を記載するまでもないと判断した問題に関しては、解説を記載せず解答のみを記載しています。もし、この問題の解説が欲しいというのがあれば、コメント欄に記載してください。また、記載している解説の内容も不明であれば遠慮なくコメントください。

