問1、問3~問4に関しては以下のページに解説をまとめているので参考にして下さい。
次の文章題の答えとして正しいものをア~オの中から1つ選び、記号で答えなさい。
[問題1] あるイベントの来場者が長いすに座っていく。長いす1脚につき4人ずつ座ると7脚足りない。また、1脚につき5人ずつ座っていくと、残りの12脚には4人ずつ座ることができた。このときのイベントの来場者数を求めなさい。
[解答群]
ア 58人 イ 93人 ウ 158人 エ 203人 オ 188人
[問題2] ある本を、1日目に全体の25%読み、2 日目には残りの51を読んだら、120ページ残った。この本は全部で何ページありますか。
[解答群]
ア 200 ページ イ 215 ページ ウ 155 ページ エ 320 ページ オ 180 ページ
[問題3] 図のxの角度を求めなさい。
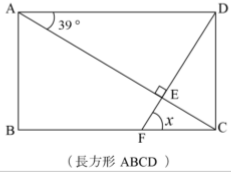
[解答群]
ア 48° イ 51° ウ 55° エ 61° オ 39°
[問題4] 丸テーブルに父母と子供4人の6人が座りたい。テーブルの座席には、図のように①~⑥の番号がつけられている。父母が隣同士 になるように座るとき、6人が座る座り方は何通りありますか。
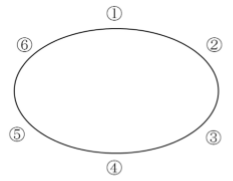
[解答群]
ア 156通り イ 240通り ウ 288通り エ 96通り オ 512通り
[問題5] 100円玉2枚と10円玉2枚を投げて、表になった金額の合計が110円以上になる確率を求めなさい。
[解答群]
ア 7/16 イ 5/8 ウ 1/4 エ 5/12 オ 1/8
解答と解説
試験問題1の解答:オ
求めたい来場者数をM、長椅子の数をNと仮定します。
長椅子1脚につき4人ずつ座ると7脚足りないということなので次の式が成り立ちます。
M=4N+4×7
=4N+28 ・・・(1)
次に1脚につき5人ずつ座っていくと、残り12脚には4人ずつ座ることができたということから次の式が成り立ちます。
M=5x(N-12)+4×12
=5N-60+48
=5N-12 ・・・(2)
式(1)(2)より、求めたい来場者数Mの人数を算出します。
M=4N+28 ・・・(1)
M=5N-12 ・・・(2)
式(1)の両辺に5、式(2)の両辺に4をかけてNの係数を揃えます。
5M=20N+140 ・・・(1)
4M=20N-48 ・・・(2)
式(1)-式(2)をするとMの値が求まります。
5M=20N+140 ・・・(1)
4M=20N-48 ・・・(2)
————————
M=188
よって、来場者数は188人
試験問題2の解答:ア
求めたい本の総ページ数をMと仮定します。
1日目に読んだのが全体の25%ということより、その読んだページ数は次の通り。
1日目に読んだページ数
Mx0.25=0.25M
1日目で読んだページ数が0.25Mなので、その時点で残っているページ数は総ページ数Mから0.25Mを引いた値になります。更に2日目でその残りページの1/5を読んだということなので、2日目に読んだページ数は次の通り。
2日目に読んだページ数
(M-0.25M)x(1/5)=0.15M
2日目で読み終わった時点で120ページが残ったということなので次の式が成り立ちます。
M=0.25M+0.15M+120
0.6M=120
M=200
よって、本の総ページ数は200ページ
試験問題3の解答:イ
三角形AEDの内角についてみていきます。
∠EAD=39°
∠AED=90°
よって、∠ADEは次の通り。
∠ADE=180-90-39=51°
四角形ABCDは長方形なので辺ADと辺BCは平行になります。辺ADと辺BCが平行の場合、∠ADE=∠CFEが成り立ちます。よって、∠CFE(x)の角度は51°となります。
x=51°
試験問題4の解答:ウ
父が右側、母が左側に座る場合、父母が隣り合って座る組み合わせ数は、全部で6通りになります。しかし、父が左側、母が右側と逆に座ることもあり得るので父母が隣り合って座る組み合わせ数は6×2=12通りとなります。
更に残り4席に子供4人が座る組み合わせ数は次の通り。
4!=4x3x2x1=24
よって、そう組み合わせ数は次の通り。
24x12=288通り
試験問題5の解答:イ
100円玉2枚と10円玉2枚の合計4枚を投げて裏表がでる総組み合わせ数は次の通り。
2x2x2x2=16通り
更に合計金額が110円以上になるには、最低限100円玉1枚が表、10円玉1枚が表となる必要があります。4枚の硬貨を100円A、100円B、10円A、10円Bとした場合、110円以上になる組み合わせは次の10通りのみになります。
100円A、10円A
100円A、10円B
100円B、10円A
100円B、10円B
100円A、10円A、10円B
100円B、10円A、10円B
100円A、100円B、
100円A、100円B、10円A
100円A、100円B、10円B
100円A、100円B、10円A、10円B
よって、求める確率は次の通り。
10/16=5/8
※解説を記載するまでもないと判断した問題に関しては、解説を記載せず解答のみを記載しています。もし、この問題の解説が欲しいというのがあれば、コメント欄に記載してください。また、記載している解説の内容も不明であれば遠慮なくコメントください。

