この問題は平成28年4月入校の東京都立職業能力開発センター入校選考試験問題の問2と問3の解答と解説です。
問1、問4~問6に関しては以下のページに解説をまとめているので参考にして下さい。
- 東京 職業訓練 試験問題[学力検査] 数学-問1(平成28年04月生)
- 東京 職業訓練 試験問題[学力検査] 数学-問4(平成28年04月生)
- 東京 職業訓練 試験問題[学力検査] 数学-問5(平成28年04月生)
- 東京 職業訓練 試験問題[学力検査] 数学-問6(平成28年04月生)
実際の試験の問題用紙は以下のページで確認することができます。
問2 試験問題
ノートを生徒に配ります。1人4冊ずつ配ると15冊あまり、5冊ずつ配ると7冊足りません。もとのノートは何冊ですか。
以下は解答と解説です。解答、解説を見る前にまずは自分自身で解けるか試してみてください。
解答と解説
試験問題2の解答:103冊
生徒の人数をM、求めたいもとのノートの冊数をNと仮定します。
1人4冊ずつ配ると15冊余るということなので次の式が成り立ちます。
N=4×M+15・・・①
さらに5冊ずつ配ると7冊足りないということなので次の式が成り立ちます。
N=5×M-7・・・②
①式の両辺に5、②式の両辺に4を掛けてMの係数を揃えます。
5N=20M+75・・・①
4N=20M-28・・・②
①-②をします。
5N-4N=(20M+75)-(20M-28)
N=103
よって、求めたい元のノートの冊数は103冊
問3 試験問題
下図のcosαの値を分数で求めなさい。
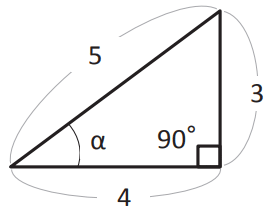
以下は解答と解説です。解答、解説を見る前にまずは自分自身で解けるか試してみてください。
解答と解説
試験問題2の解答:4/5
この問題は直角三角形のcosθの求め方である以下の点を知っていればものの数秒で解ける問題です。

実際に直角三角形に当てはめると下図のようになります。
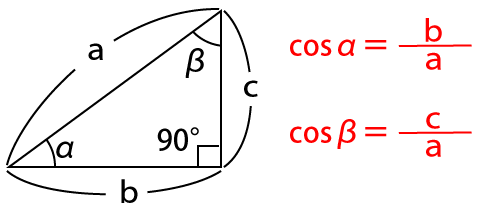
よって、今回の問題であれば直角な角の対辺は5、∠αと直角な角に接する辺の長さは4なので、cosαは次のようになります。
cosα=4/5
※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。

