東京 職業訓練 試験問題[学力検査] 数学-問4,問5(平成26年4月生)

問４ 試験問題

ある図書館の12月の利用者数は、子供と大人を合わせて7.980人でした。 1月の利用者数は12月と比べて、子供は30%増加し、大人は5%減少したところ、子供が大人よりも924人多くなりました。このとき、この図書館の1月の子供の利用者数は何人ですか。

解答と解説

試験問題４の解答：4,914人

12月の子供も利用者数をＮと仮定した場合、12月と1月の子供と大人の利用者数は以下のようにあらわすことができます。

12月子供の利用者数：Ｎ
12月大人の利用者数：7980－Ｎ
1月子供の利用者数：Ｎ×1.3
1月大人の利用者数：(7980－Ｎ)×0.95

1月の子供の利用者数は1.3、大人の利用者数は0.95を掛けている理由は分かりますよね？
子供の30％増加ということは、12月の130％の人数ということになるので130％＝1.3を掛けています。大人は5％減なので12月の95％の人数ということになるので95％＝0.95を掛けています。

問題文より1月の子供の利用者数は大人よりも924人多いということなので次の式が成り立ちます。

1月の子供の利用者数＝1月の大人の利用者数＋924
Ｎ×1.3＝(7980－Ｎ)×0.95＋924
1.3Ｎ＝7581－0.95Ｎ＋924
1.3Ｎ＋0.95Ｎ＝7581＋924
2.25Ｎ＝8505
Ｎ＝3780

よって、12月の子供の利用者数は3780人。しかし、求めたいのは1月の子供の利用者数なので、次のようになります。

1月子供の利用者数：Ｎ×1.3
3780×1.3
＝4914

よって、1月の子供の利用者数は4,914人

問５ 試験問題

表のように、自然数1、2、3、4、・・・を規則的に並べたとき、15行の5列目に入る数字を求めなさい。

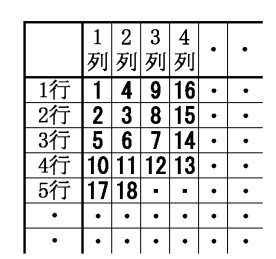
解答と解説

試験問題５の解答：201

規則性を見つけられるかどうかがこの問題のポイントとなります。

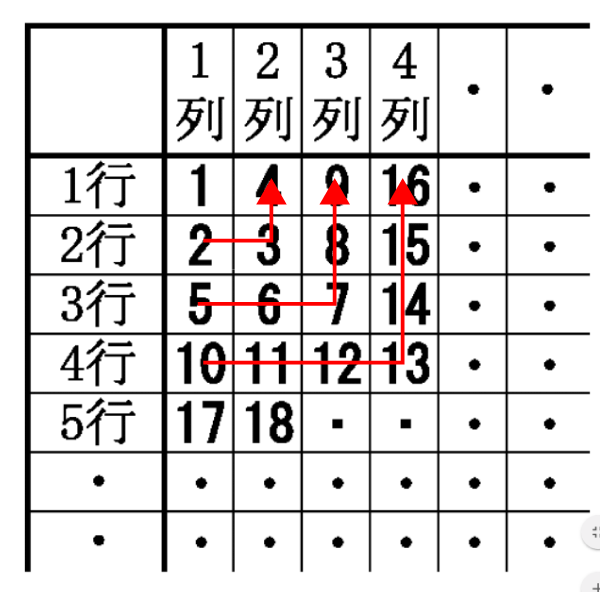
表内の数字は上表のように2行2列、3行3列、4行4列・・・のように同じ行列数で折り返しています。

よって、15行目も15列目までは折り返さないことが分かるので、まずは1列目の15行目の数値を導き、その数に4を加えた値が15列目の値になります。

そこで、まずは1列目の規則性を考える必要があります。1列目は、1,2,5,10,17・・・と増えていっており、その増分は1,3,5,7・・・と規則性があることが分かります。

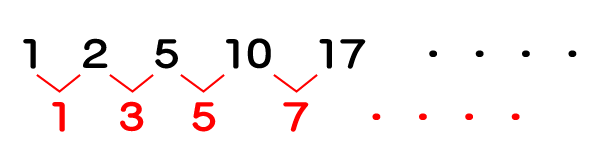
15行目なのでそのまま力技で求めていってもさほど時間はかかりませんが、この規則性を式に直すと次のようになります。

1列目の規則性＝2ｎ－1

この規則性の式はできれば頭の中で導き出せるようにしておきたいところですが、どうしても導き出せないという方は以下の公式を覚えておいてください。

1列目の14行目と15行目の差分は、増分としては14番目になるので規則性の式より、次のようになります。

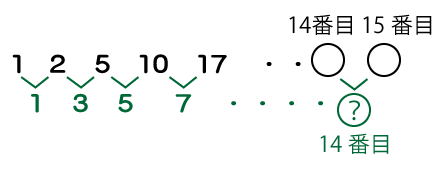
1列目14番目の増分値＝2ｎ－1
　　　　　　　　　＝2×14－1
　　　　　　　　　＝27

ここでもう1点知っておくべき知識があります。それは、下記例のように規則性を持って並んだ数値の1番目の数値と一番最後の数値を足した数、さらに2番目の数値と最後から2番目に足した数、以降同様にすべて同じ数になるという点です。

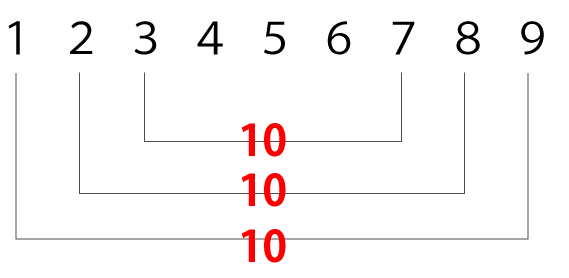
よって、1番目目の増分値1と最後の14番目の増分値27を足すと28となります。この28の数値が全部で7つあることになります(14つの増分の前後を足しているので14÷2＝7)。

これにより、増分の合計は『28×7＝196』だと分かります。

よって、15行目の1列目は『196＋1＝197』となります。

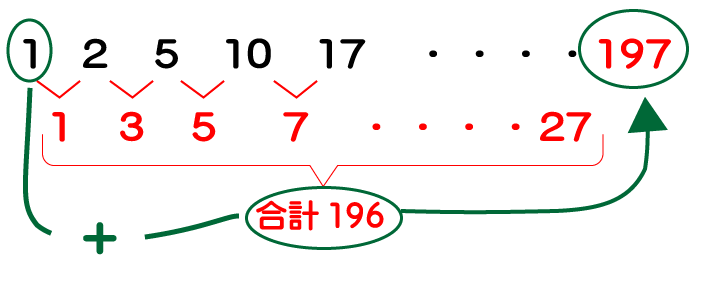
これにより、15行目の5列目は、『197＋4＝201』となります。

※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。