この問題は平成26年4月入校の東京都立職業能力開発センター入校選考試験問題の問６の解答と解説です。

問１～問５に関しては以下のページに解説をまとめているので参考にして下さい。

実際の試験の問題用紙は以下のページで確認することができます。

⇒都立職業能力開発センター入校選考試験問題(平成26年04月生)

問題を解くのに必要な知識

  • 円柱の体積を求める公式

問６ 試験問題

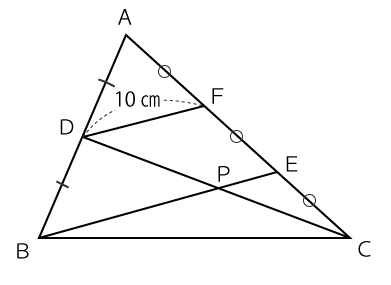
図のように、△ABCのAB上にAD＝BDとなる点Dをとり、CA上にCE＝EF＝FAとなる点E、Fをとります。また、BEとCDの交点をPとします。DFの長さは10cmのとき、BPの長さは何cmですか。

三角形

解答と解説

試験問題６の解答：15㎝

この問題を解くには三角形の相似条件を知っている必要があります。

三角形の相似条件

  1. ３組の辺の比がすべて等しい
  2. ２組の辺の比とその間の角がそれぞれ等しい
  3. ２組の角がそれぞれ等しい

BEの長さを求める

△ADFと△ABEは∠Aが共通で、∠Aと接する2辺の比が等しいので上記相似条件『２組の辺の比とその間の角がそれぞれ等しい』を満たしており、相似な三角形になります。

問題文よりAF＝FEと分かっています。
よって、AEはAFの2倍の長で△ADFと△ABEの相似比は『１：２』となります。

△ADF：△ABE＝１：２

相似な三角形の各辺の比は等しいので『BE＝2DF』となります。よって、BEの長さは次の通り。
BE＝10×2＝20cm

EPの長さを求める

同様に△CEPと△CFDも相似条件『２組の辺の比とその間の角がそれぞれ等しい』を満たしており、相似な三角形になります。

問題文よりCE＝FEと分かっています。
よって、CFはCEの2倍の長で△CEPと△CFDの相似比は『１：２』となります。

△CEP：△CFD＝１：２

相似な三角形の各辺の比は等しいので『FD＝2EP』となります。よって、EPの長さは次の通り。
EP＝FD÷2
　＝10÷2
　＝5㎝

BPの長さを求める

BEの長さが20cm、EPの長さが5㎝と分かったので、求めたいBPの長さは次の通り。

BP＝BE－EP
　＝20－5
　＝15㎝

よって、求めたいBPの長さは15㎝

※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。