この問題は平成25年4月入校の東京都立職業能力開発センター入校選考試験問題の問4と問5の解答と解説です。
問1~問3、問6に関しては以下のページに解説をまとめているので参考にして下さい。
- 東京 職業訓練 試験問題[学力検査] 数学-問1(平成25年04月生)
- 東京 職業訓練 試験問題[学力検査] 数学-問2,問3(平成25年04月生)
- 東京 職業訓練 試験問題[学力検査] 数学-問6(平成25年04月生)
実際の試験の問題用紙は以下のページで確認することができます。
問4 試験問題
ろうそくに火をつけると、一定の割合で短くなっていきます。火をつけてから7分後の長さは18cm、25分後の長さは10cmでした。ろうそくが燃え尽きて消えてしまうのは、火をつけてから何分何秒後ですか。
解答と解説
試験問題4の解答:47分30秒
ろうそくの長さは、火をつけてから7分後が18㎝、25分後が10㎝なので、18分間の間に8㎝燃え尽きたということが分かります。
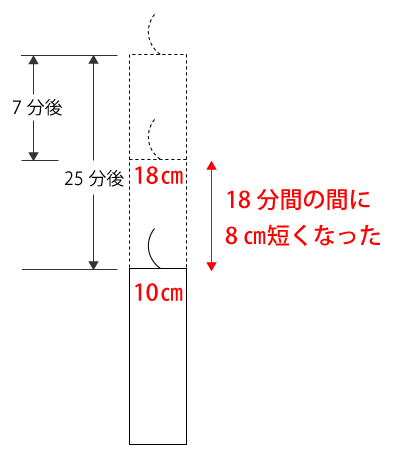
よって、1㎝燃えるのにかかる時間は次の通り。
1㎝燃えるのにかかる時間=(18×60)÷8
=135秒
※上記計算は分を秒になおすために18×60をしています。分のままで計算しても構いませんが、18÷8=2.25分となり、0.25って何秒ってなる人は上の式のように秒になおして計算する方がいいかと思います。
1㎝燃えるのにかかる時間に135秒かかると分かりました。よって、ろうそくの残り10㎝が燃え尽きるのにかかる時間は次の通り。
10㎝が燃え尽きるのにかかる時間=10×135
=1350秒
=22分30秒
よって、火をつけてから完全に燃え尽きるまでの時間は次の通り。
火をつけてから燃え尽きるまでの時間=25分+22分30秒
=47分30秒
解答の補足
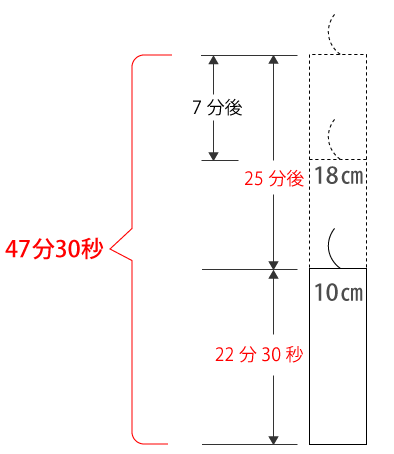
火をつけてから燃え尽きるまでの時間を『7分+25分+22分30秒=54分30秒』と間違えないようにしましょう。下図のように7分は25分の中に含まれています。
問5 試験問題
下図のような、1、2、3の数字を記したカード各2枚、合計6枚が袋の中に入っています。この中から2枚同時に取り出すとき、2枚のカードの数字の和が素数になる確率を分数で求めなさい。
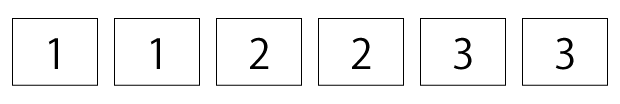
解答と解説
試験問題5の解答:3/5
この問題を解くには次の2点を知っている必要があります。
問題を解くのに必要な知識
- 素数とは何か?
- 組み合わせの公式
素数とは、1と自分自身同じ数字以外で割れない自然数のことです。たとえば、「3」や「5」、「7」、「11」といった数字です。これらの数字は1とその数字でしか割ることができません。
次に組み合わせの公式ですが、公式は次の通りです。

今回のような問題であれば、最悪、組み合わせの公式を知らなくても力技で1つずつ数えていくことも可能ですが、問題によっては簡単に数えられない場合もあるので覚えておくようにしましょう。
取り出した2枚のカードの数字の和が素数になる確率は次の式で表すことができます。
素数になる確率=(和が素数になる組み合わせ数)/(全組み合わせ総数)
6枚のカードから2枚の取り出す全組み合わせ総数は、組み合わせの公式より次の通り。
₆C₂=(6×5×4×3×2×1)/{(2×1)(4×3×2×1)}
真面目に計算せず、まずは約分できるところまで約分を行い計算を簡略化しましょう。
₆C₂=(6×5)/(2×1)
=3×5
=15
よって、全組み合わせ数は15通り。
次に和が素数になる組み合わせ数ですが、これは1つずつ確認していきます。
1+1=2(素数)
1+2=3(素数)
1+2=3(素数)
1+2=3(素数)
1+2=3(素数)
1+3=4
1+3=4
1+3=4
1+3=4
2+2=4
2+3=5(素数)
2+3=5(素数)
2+3=5(素数)
2+3=5(素数)
3+3=6
和が素数になる組み合わせは全部で上記の9通りあります。
解説ではあえて組み合わせの公式を使って全組み合わせ数の出しましたが、上記のように素数の組み合わせ数を確認するさいに全組み合わせを洗い出す場合は、公式を使って組み合わせ数を出す必要はありません。
よって、2枚のカードの数字の和が素数になる確率は、9/15=3/5
※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。

